The Side Angle Side postulate (often abbreviated as SAS) states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then these two triangles are congruent.
Example
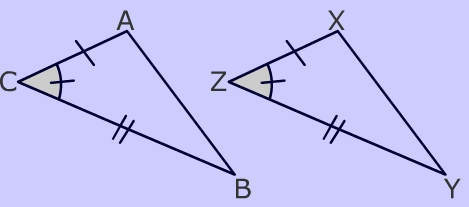
$$ \triangle ABC \cong \triangle XYZ $$
- Two sides and the included angle are congruent
- AC = ZX (side)
- $$ \angle $$ACB = $$ \angle $$XZY (angle)
- CB = ZY (side)
- Therefore, by the Side Angle Side postulate, the triangles are congruent.
Included Angle
The included angle means the angle between two sides. In other words it is the angle 'included between' two sides.
Identify Side Angle Side Relationships
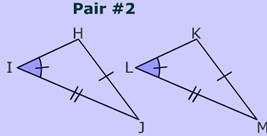
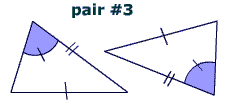

Pair four is the only true example of this method for proving triangles congruent. It is the only pair in which the angle is an included angle.
Side Angle Side Practice Proofs
Side Angle Side Example Proof
Prove: $$ \triangle BCD \cong \triangle BAD $$

Given: HJ is a perpendicular bisector of KI

Side Angle Side Activity
Below is the proof that two triangles are congruent by Side Angle Side.
Can you imagine or draw on a piece of paper, two triangles, $$ \triangle BCA \cong \triangle XCY $$ , whose diagram would be consistent with the Side Angle Side proof shown below?

-
Theorems and Postulates for proving triangles congruent:
- Hypotenuse Leg Theorem
- Side Side Side
- Side Angle Side
- Angle Side Angle
- Angle Angle Side
- isosceles triangle proofs
- CPCTC
- indirect proof
- quiz on all theorems/postulates
- Images















