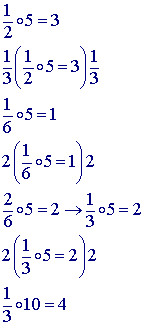Logic Games And Riddles
How can you add eight 8's to get the number 1,000? (only use addition).
The key to this math riddle is realizing that the one place must be zero. 888 + 88 + 8 + 8 + 8 = 1,000.
One of the 'fathers' is also a grandfather. Therefore the other father is both a son and a father to the grandson.
In other words, the one father is both a son and a father.
The most common digit is '1.' Can you figure out why? No hints until you try the next riddle because the next riddle is closely tied to this one.
Part II. What digit is the least frequent between the numbers 1 and 1,000?
0 is the least common digit even though 1,000 has three zero's!
Explanations for both riddles
The digits 0 through 9 all follow the same pattern there is exactly 1 occurrence of each digit for every ten numbers.
Again, let's look at 2 which appears in 20, 21, 22, 23, etc.. as well as 200, 201, 202, 203.
So to figure out how to answer the first riddle you had to see what distinguishes the number 1? Only that we are including 1,000 which would be the first '1' in a new series of ten! In other words, the digit 1 only has a single extra occurrence (301 occurrences) compared to 2 or 3 or 9 which each have exactly 300 occurrences.
The reason that zero has the least (BY FAR at only 192 occurrences) is because zero does not have any equivalents to 22, 33, 44, 222, 3333 etc.
There are many ways of explaining/thinking about this truly brain bending riddle! It all boils down to the fact that the lawyers's math is incorrect.
They did NOT spend $$\$9$$ • 3 + $$\$2$$.
They spent exactly $$\$27$$ dollars. $$\$25$$ for the room and $$\$2$$ for the tip. Remember they got exactly $$\$3$$, in total back.
Another way to think about the answer to this riddle is to just pretend that the bellhop refunded $$\$3$$ to the lawyers (rather than giving them $$\$5$$ and receiving $$\$2$$ back).
If the lawyers get $$\$3$$ back and each takes $$\$1$$. Then they spent exactly $$\$27$$ dollars.
The answer is 4.
11 cartons total
7 large boxes (7 * 8 = 56 boxes)
4 small boxes (4 10 = 40 boxes
11 total cartons and 96 boxes
The key to solving this riddle is realizing that you have to take the rabbit over first and the switch the fox with the rabbit. See step 2.
Step 1Take the rabbit to the other side.
| Shore | Other Side |
| Carrots Fox |
Rabbit |
Go back and get the Fox and switch it with the Rabbit.
**The key here is that the carrots and the rabbit are not being left alone.
| Shore | Other Side |
| Carrots Rabbit (Not left alone) |
Fox |
Take the carrots across.
| Shore | Other Side |
| Rabbit | Fox Carrots |
Go back and get the rabbit.
| Shore | Other Side |
| Rabbit Fox Carrots |
Every farmer's part is $$1/3(45+75) = 40$$ sacks.
Charlie paid $$\$1400$$ for $$40$$ sacks, then 1 sack costs $$\$1400/40 = $35/{\text{sack}}$$.
Adam got $$\$35*(45-40)=35*5 = \$175$$.
Ben got $$\$35*(75-40)=35*35 = \$1225$$.
Answer: Ben $$\$1225$$, Adam $$\$175$$
Why would he need to go back to get the last hint after seeing the number on the house next door?
Because the sum of their ages (the number on the house) is ambiguous and could refer to more than 1 trio of factors.
{2, 2, 9}
If you list out the trio of factors that multiply to 36 and their sums, you get:
Since the number on the house next door is not enough information there must be more than 1 factor trio that sums up to it, leaving two possibilities: { 6, 6, 1} , {2, 2, 9} . When she says her 'oldest' you know it can not be {6, 6, 1} since she would have two 'older' sons not an 'oldest'.
This is a famous one. The classic Monty hall riddle!
The Situation:You are confronted by 3 doors. Behind one of them is a car, behind the two others, you will only see a goat. Now, if you correctly pick the car, you win the car! Otherwise, if you get one of the 2 goats, you don't get the car.
So, pick any door. It doesn't matter which one, but we will suppose that you picked door #2, as an example.
Now, after you have picked a door and before finding out what is actually behind it, you are shown a goat behind one of the other doors. (Remember there has to be a goat in 1 of the doors that you have not picked.)
Let's say you choose door #2, as shown above. For example's sake, let's say there's a goat in door 1. The question and the riddle is: should you switch the door that you picked? In other words, in this example, should you now choose door 3? Or, should you stick with your first choice (door #2)?
There actually is a mathematically correct answer to this riddle: You should indeed change your choice. If you don't believe me, just try out our free online Monty hall simulation.
Look at how many closed areas there are.
An athlete is able to jump FOREVER. However, everytime that she jumps she gets a bit more tired, and every jump goes $$ \frac 1 2 $$ as far as her prior jump. Now, for her very first jump, she goes $$ \frac 1 2 $$ of a foot.
On her second jump, she goes $$ \frac 1 4 $$ of a foot, and so on and so forth. The beginning of her journey is shown in the gif below.
She will never get to the 1 foot mark because you keep adding smaller and smaller amounts!
Zeno's paradox of Achilles and the Tortoise
Quick summary of riddle: Zeno of Elea (490-425 BC) is known for creating many paradoxes which were debated by mathematicians for centuries. His riddle involving Achilles, the character from Homer's Iliad and a tortoise went something like:
The tortoise challenged Achilles to a race and Achilles, full of typical hubris, accepted and even gave the Tortoise a 10 foot head start. Before the race started, the tortoise told Achilles that the reason Achilles would lose is that even though Achilles would be catching up, the tortoise would always be moving ahead. Therefore, Achilles would always be covering a fraction of the distance between the two. Let's say he covered half of the distance in 1 second (5 feet) and then in the next he covered half of the new distance, the remaining 5 feet plus the Tortoise's new distance. In the end, the tortoise convinced Achilles that he could not win the race because although he would be getting closer and closer, he would still always be covering smaller and smaller fractions of the total distance between the two. Therefore, Achilles forfeited the race. To read this riddle in a modern narrative form click here.
Your First Choice
Should You switch?
