Midpoint Of A Line -Examples , video lesson explained with cool applet and pictures

Video Tutorial on Mid Point

Examples

Example 1

Find midpoints from 2 endpoints

What is the midpoint of A (2, 14) and B (4, 6)?

$$ A (\color{Red}{2}, \color{Green}{14}) \text{ and }B (\color{Red}{4}, \color{Green}{6}) \\ Midpoint = \Big(\frac{ \color{Red}{x_2 + x_1}}{2}, \frac{\color{Green}{y_2 + y_1}}{2} \Big) \\ \Big( \frac{\color{Red}{2 + 4} }{ 2}, \frac{\color{Green}{14 + 6} }{ 2} \Big) = \Big( \frac{ 6 }{ 2}, \frac{ 20 }{ 2} \Big) \\ Midpoint = (3, 10) $$

Example 2

Find end point from midpoint and other end point

If point X, the midpoint of segment AB, has coordinates (-4, 9) and the coordinates of point A are (1, 3), what are the coordinates of point B?

Practice Problems

Problem 1

What is the midpoint of segment AB, given A (1, 2) and B (7, 4)?

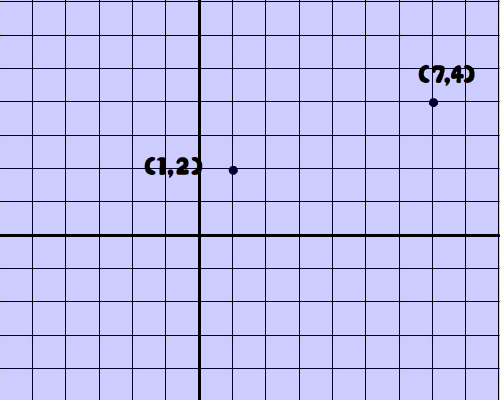
Problem 2

What is the midpoint of A (4, 7) and B (-8, 15)?

This is like example 1 above.

$$ A (\color{Red}{4}, \color{Green}{ 7 }) \text{ and }B (\color{Red}{-8}, \color{Green}{ 15 }) \\ Midpoint = \Big(\frac{ \color{Red}{x_2 + x_1}}{2}, \frac{\color{Green}{y_2 + y_1}}{2} \Big) \\ \Big( \frac{\color{Red}{4 + -8} }{ 2}, \frac{\color{Green}{7 + 15} }{ 2} \Big) = \Big( \frac{ -4}{ 2}, \frac{22}{ 2} \Big) \\ Midpoint = (-2,11) $$

Problem 3

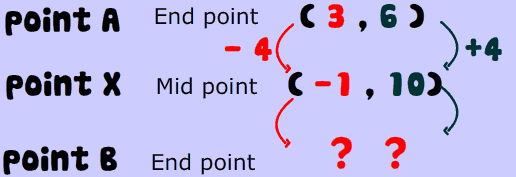
If point X, the midpoint of segment AB, has coordinates(-1, 9) and the coordinates of point A are (3, 7), what are the coordinates of point B?

Calculate how far you 'went' from the given endpoint to the midpoint (we went -4 in x and +4 in y).

Go the same amount in the x and y directions.

Problem 4

What is the midpoint of A (-2, 3) and B (-10, 12)?

This is like example 2 above.

$$ A (\color{Red}{-2}, \color{Green}{ 3 }) \text{ and }B (\color{Red}{-10}, \color{Green}{ 12 }) \\ Midpoint = \Big(\frac{ \color{Red}{x_2 + x_1}}{2}, \frac{\color{Green}{y_2 + y_1}}{2} \Big) \\ \Big( \frac{\color{Red}{-2 + -10} }{ 2}, \frac{\color{Green}{3 + 12} }{ 2} \Big) = \Big( \frac{ -12}{ 2}, \frac{15}{ 2} \Big) \\ Midpoint = (-6,7.5) $$

Midpoint Worksheet

Midpoint Calculator

Midpoint Applet