Indirect Proof

Indirect proof is synonymous with proof by contradiction. A keyword signalling that you should consider indirect proof is the word 'not'. Usually, when you are asked to prove that a given statement is NOT true, you can use indirect proof by assuming the statement is true and arriving at a contridiction.The idea behind the indirect method is that if what you assumed creates a contradiction, the opposite of your initial assumption is the truth.

Example of an Indirect Proof

Prove that $$ \angle $$BDA is not a straight angle.

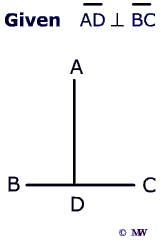
Statement	Reason
1) $$ \angle $$BDA is a straight angle	1) (Assume opposite)
2) m $$ \angle $$BDA = 180°	2) Definition of a straight angle
3) AD $$ \perp $$ BC	3) Given
4) $$ \angle $$BDA is a right angle	4) Definition of perpendicular lines
5) m $$ \angle $$BDA = 90°	5) Definition of a right angle
6) m $$ \angle $$BDA is not a straight angle	6) Contradiction of steps 2 and 5
7) $$ \angle $$BDA is not a straight angle	7) Due to the contradiction between 2 and 5, we know that the assumption that WE INTRODUCED in the first step ($$ \angle $$bda is a straight angle) is false. Therefore, the opposite must be true: $$ \angle $$ is not a straight angle.