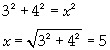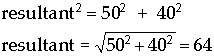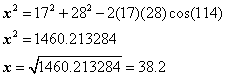Resultant Vector, how to calculate a resultant using the parallelogram method and the head to tail method. A resultant is simply...

This Page:

The resultant vector is the vector that 'results' from adding two or more vectors together. There are a two different ways to calculate the resultant vector.

Methods for calculating a Resultant Vector:

The head to tail method to calculate a resultant which involves lining up the head of the one vector with the tail of the other.
The parallelogram method to calculate resultant vector. This method involves properties of parallelograms but, in the end, boils down to a simple formula.

In the picture on the left, the black vector is the resultant of the two red vectors. To try to understand what a resultant is consider the following story.

If you drove from your house, centered at the origin. To your friends house, at the point (3, 4), imagine that you had to take two different roads these are the two red vectors. However, the resultant vector vector would be the straight line path from your home to your friend's house, and the black vector represents that path.

Head to Tail Method

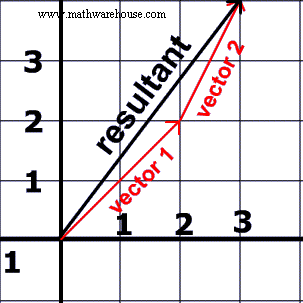
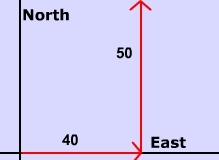
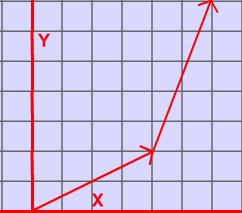
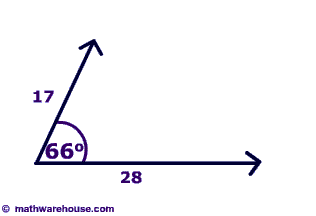
The head to tail method is way to find the resultant vector. The steps are quite straight forward. The head to tail method considers the head of a vector to be the end with the arrow, or the 'pointy end'. The tail of the vector is where the vector begins.

Place the two vectors next to each other such that the head of the one vector is touching the tail of the other vector.
Draw the resultant vector by starting where the tail of first vector is to the head of second vector.

Steps for Head to Tail Method

Calculate the magnitude resultant vector

Find the sum of each pair of vectors (the magnitude of the resultant vector).

To find the resultant vector's magnitude, use the pythagorean theorem.

Practice Problems

Problem 1

You left your house to visit a friend. You got in your car drove 40 miles east, then got on a highway and went 50 miles north.

Draw a vector from the beginning of your journey, your home, and the end, your friend’s house.

How long is the vector that you drew?

Problem 2

What is the sum of the two vectors? Use the head to tail method to calculate the resultant vector in the picture on the right.

Parallelogram Method to Calculate Resultant

Before tackling the parallelogram method for solving resultant vectors, you should be comfortable with the following topics.

SOHCAHTOA (basic sine, cosine, tangent)
Law of Cosines
Law of Sines
The Following Properties of Parallelograms

Opposite Sides of Parallelograms are Congruent
Opposite Angles of Parallelograms are Congruent

Problem 3

To best understand how the parallelogram method works, lets examine the two vectors below. The vectors have magnitudes of 17 and 28 and the angle between them is 66°. Our goal is to use the parallelogram method to determine the magnitude of the resultant.

Step 1

Draw a parallelogram based on the two vectors that you already have. These vectors will be two sides of the parallelogram (not the opposite sides since they have the angle between them).

Step 2

We now have a parallelogram and know two angles (opposite angles of parallelograms are congruent). We can also figure out the other pair of angles since the other pair are congruent and all four angles must add up to 360.

Step 3

Draw the paprallelograms diagonal. This diagonal is the resultant vector.

Step 4

Use the law of cosines to determine the length of the resultant.

Use the law of cosines to calculate the resultant.