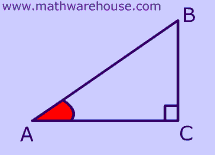
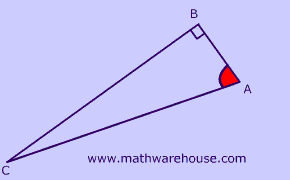
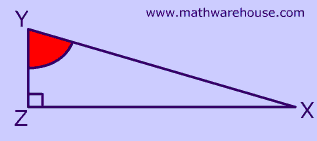
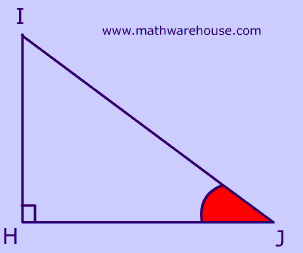
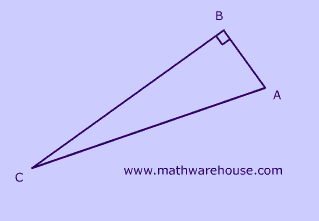
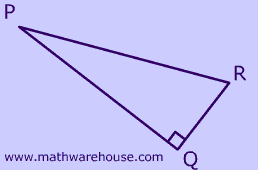
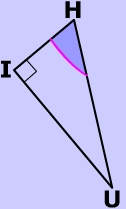
To which triangle(s) below does SOHCAHTOA apply?
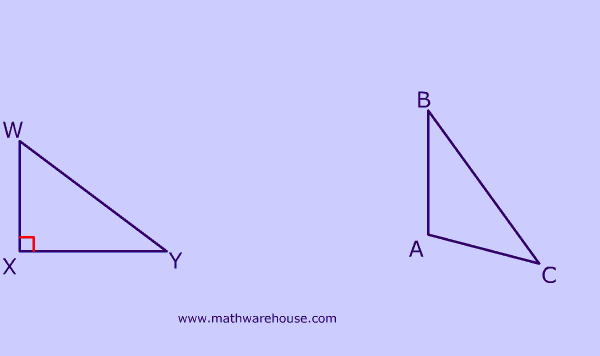
Opposite & adjacent sides and SOHCAHTOA of angles
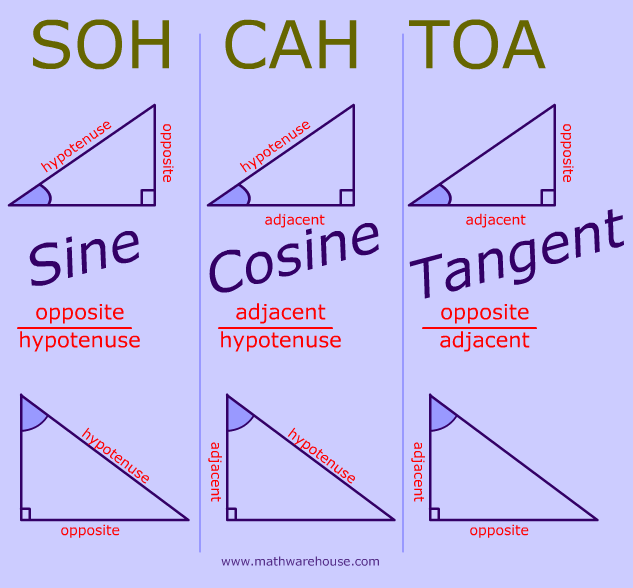
This page explains the sine, cosine, tangent ratio, gives on an overview of their range of values and provides practice problems on identifying the sides that are opposite and adjacent to a given angle.
The Sine, Cosine and Tangent functions express the ratios of sides of a right triangle.
Try activating either $$ \angle A $$ or $$ \angle B$$ to explore the way that the adjacent and the opposite sides change based on the angle.
|
|
|
Answer: sine of an angle is always the ratio of the $$\frac{opposite side}{hypotenuse} $$.
$ sine(angle) = \frac{ \text{opposite side}}{\text{hypotenuse}} $
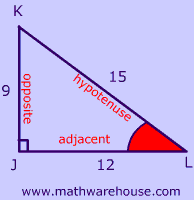
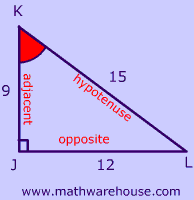
$$ sin(\angle \red L) = \frac{opposite }{hypotenuse} \\ sin(\angle \red L) = \frac{9}{15} $$
$$ sin(\angle \red K) = \frac{opposite }{hypotenuse} \\ sin(\angle \red K)= \frac{12}{15} $$
Remember: When we use the words 'opposite' and 'adjacent,' we always have to have a specific angle in mind.
For those comfortable in "Math Speak", the domain and range of Sine is as follows.
The sine of an angle has a range of values from -1 to 1 inclusive. Below is a table of values illustrating some key sine values that span the entire range of values.
| Angle | Sine of the Angle |
| 270° | sin (270°) = -1 (smallest value that sine can have) |
| 330° | sin (330°) = -½ |
| 0° | sin(0°) = 0 |
| 30° | sin(30°) = ½ |
| 90° | sin(90°) = 1 (greatest value that sine can have) |
The cosine of an angle is always the ratio of the (adjacent side/ hypotenuse).
$ cosine(angle) = \frac{ \text{adjacent side}}{\text{hypotenuse}} $
$$ cos(\angle \red L) = \frac{adjacent }{hypotenuse} \\ cos(\angle \red L) = \frac{12}{15} $$
$$ cos(\angle \red K) = \frac{adjacent }{hypotenuse} \\ cos(\angle \red K) = \frac{9}{15} $$
For those comfortable in "Math Speak", the domain and range of cosine is as follows.
The cosine of an angle has a range of values from -1 to 1 inclusive. Below is a table of values illustrating some key cosine values that span the entire range of values.
| Angle | Cosine of the Angle |
| 0° | cos (0°) = 1 (greatest value that cosine can ever have) |
| 60° | cos (60°) =½ |
| 90° | cos(90°) = 0 |
| 120° | cos(120°) = -½ |
| 180° | cos(180°) = -1 (smallest value that cosine can ever have) |
The tangent of an angle is always the ratio of the (opposite side/ adjacent side).
$ tangent(angle) = \frac{ \text{opposite side}}{\text{adjacent side}} $
$$ tan(\angle \red L) = \frac{opposite }{adjacent } \\ tan(\angle \red L) = \frac{9}{12} $$
$$ tan(\angle \red K) = \frac{opposite }{adjacent } \\ tan(\angle \red K) = \frac{12}{9} $$
Hypotenuse = AB
Opposite side = BC
Adjacent side = AC
Hypotenuse = AC
Opposite side = BC
Adjacent side = AB
Hypotenuse = YX
Opposite Side = ZX
Adjacent Side = ZY
Hypotenuse = I
Side opposite of A = H
Side adjacent to A = J
First, remember that the middle letter of the angle name ($$ \angle A \red C B $$) is the location of the angle.
Second: The key to solving this kind of problem is to remember that 'opposite' and 'adjacent' are relative to an angle of the triangle -- which in this case is the red angle in the picture.
First, remember that the middle letter of the angle name ($$ \angle R \red P Q $$) is the location of the angle.
Second: The key to solving this kind of problem is to remember that 'opposite' and 'adjacent' are relative to an angle of the triangle -- which in this case is the red angle in the picture.
First, remember that the middle letter of the angle name ($$ \angle B \red A C $$) is the location of the angle.
Second: The key to solving this kind of problem is to remember that 'opposite' and 'adjacent' are relative to an angle of the triangle -- which in this case is the red angle in the picture.
First, remember that the middle letter of the angle name ($$ \angle I \red H U $$) is the location of the angle.
Second: The key to solving this kind of problem is to remember that 'opposite' and 'adjacent' are relative to an angle of the triangle -- which in this case is the red angle in the picture.