Example of Angle Side Angle Proof
$$ \triangle ABC \cong \triangle XYZ $$
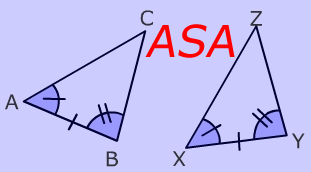
These two triangles are congruent because two sides and the included angle are congruent.
- $$ \angle CAB \cong \angle ZXY $$ (angle)
- AB $$ \cong $$ XY (side)
- $$ \angle ACB \cong \angle XZY $$ (angle)
Included Side
The included side means the side between two angles. In other words it is the side 'included between' two angles.
Identify Angle Side Angle RelationshipsIn which pair of triangles pictured below could you use the Angle Side Angle postulate (ASA) to prove the triangles are congruent?
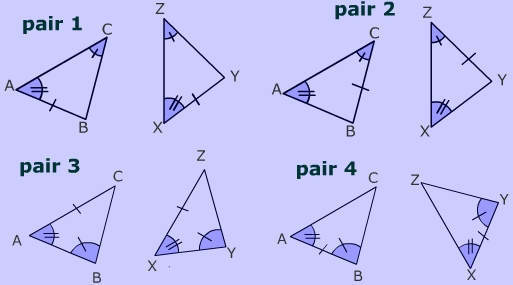
Practice Proofs
Proof 1
Prove that $$ \triangle LMO \cong \triangle NMO $$

Proof 2
Use the ASA postulate to that $$ \triangle ACB \cong \triangle DCB $$

Proof 3
Use the ASA postulate to that $$ \triangle ABD \cong \triangle CBD $$

We can use the Angle Side Angle postulate to prove that the opposite sides and the opposite angles of a parallelogram are congruent
Proof 4
Given: ABCD is a parallelogram.
Prove the opposite sides and the opposite angles of a parallelogram are congruent.
Remember the definition of parallelogram: a quadrilateral that has two pairs of opposite parallel sides.
-
Theorems and Postulates for proving triangles congruent
- Hypotenuse Leg Theorem
- Side Side Side
- Side Angle Side
- Angle Side Angle
- Angle Angle Side
- isosceles triangle proofs
- CPCTC
- indirect proof
- quiz on all theorems/postulates
- Images












