Angle Angle Side postulate for proving congruent triangles ...

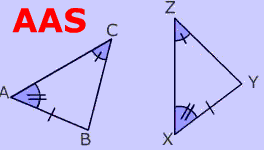
The Angle Angle Side postulate (often abbreviated as AAS) states that if two angles and the non-included side one triangle are congruent to two angles and the non-included side of another triangle, then these two triangles are congruent.

Worksheet & Activity on the Angle Angle Side Postulate

Example of Angle Angle Side Proof (AAS)

$$ \triangle $$ ABC $$ \triangle $$ XYZ

Two angles and a non-included side are congruent

$$ \angle A \cong \angle X $$ (angle)
$$ \angle C \cong \angle Z $$ (angle)
AB $$\cong$$ XY (side)

Therefore, by the Angle Angle Side postulate (AAS), the triangles are congruent.

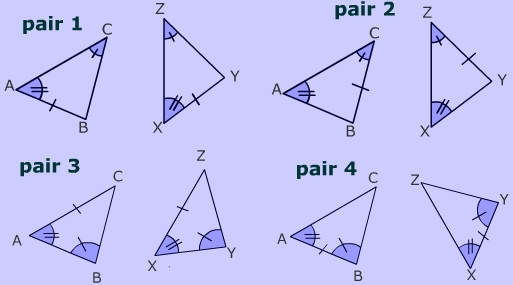
Identify Angle Angle Side relationship

Identify which pair of triangles below does NOT illustrate an angle angle side (AAS) relationship.

Problem 1

Identify the coordinates of all complex numbers represented in the graph below.

Identify Angle Angle Side relationship (AAS)

Practice Proofs

Proof 1

Prove that $$ \triangle ABC \cong \triangle DEC $$.

Proof 2

Prove that $$ \triangle ABC \cong \triangle DEF $$.

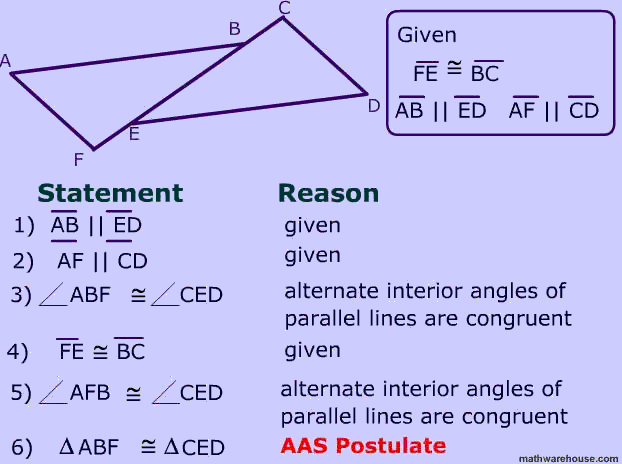
Can you identify the error in the AAS proof below?

What is wrong with the proof below?

The error involves the side needed to prove two triangles congruent by the Angle Angle Side Postulate.

FE and BC are NOT full sides in either triangle. You would need to use the additon property of equality to add segment BE to FE and BE to be able to state that their is a pair of congruent sides in the two triangles.