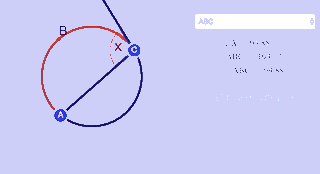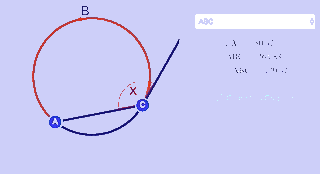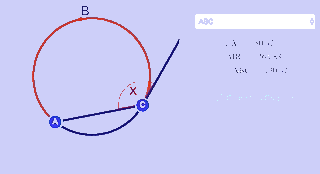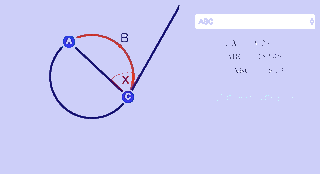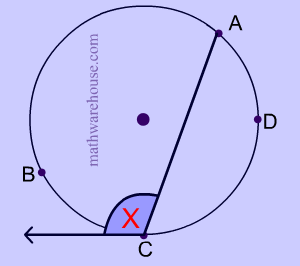
An angle formed by a chord (link) and a tangent (link) that intersect on a circle is half the measure of the intercepted arc.
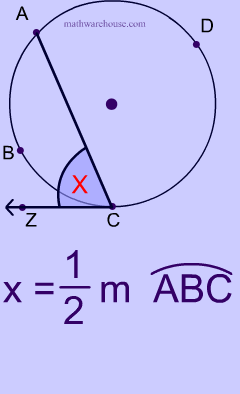
$ x = \frac 1 2 \cdot \text{ m } \overparen{ABC} $
Note: Like inscribed angles, when the vertex is on the circle itself, the angle formed is half the measure of the intercepted arc.
Interactive Applets
Practice Problems
Problem 1
Chord $$ AC $$ intercepts a tangent tangent at point C. If the measure of $$ \overparen{abc} = 70^{\circ} $$, what is x ?
Use the theorem above to find the measure of angle formed by the intersection of the tangent that intersects chord AC.
By the theorem, the measure of angle is half of the intercepted arc which is $$70 ^{\circ}$$ .
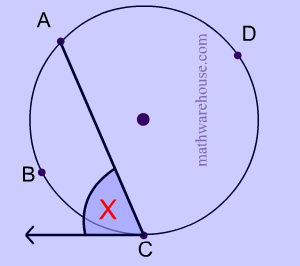
Therefore $$ x = \frac{1}{2} \cdot 70 = 35^{\circ} $$ .
Problem 2
Challenge Problems
Problem 3
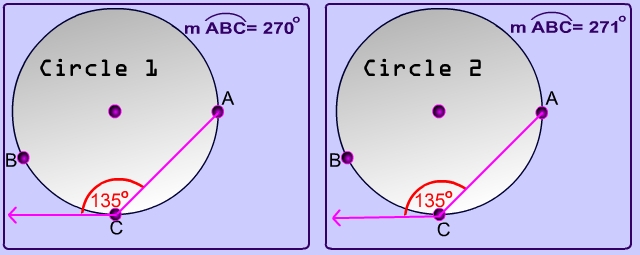
For the $$ m\overparen{ABC} $$ ? to equal ¾ the total measure of the circle's circumference, what must be the value of X?
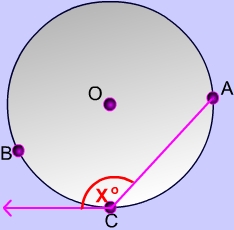
Total measure of circle's circumference = 360°.
$$ \frac 3 4 (360^{\circ}) = 270^{\circ} $$
By our theorem, we know that the angle formed by a tangent and a chord must equal half of the intercepted arc so $$x = \frac 1 2 \cdot 270^{\circ} =135^{\circ} $$ .
Problem 4
Problem 5
What is the measure of $$ \angle ACZ $$ for circle with center at O?
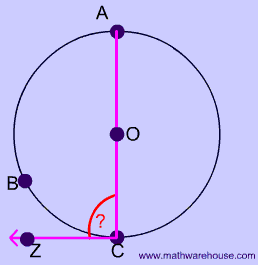
The key to this problem is recognizing that $$ \overline{AOC}$$ is a diameter.
Therefore, $$m \overparen{ABC} = 180 ^{\circ} $$.
At this point, you can use the formula, $$ \\ m \angle ACZ= \frac{1}{2} \cdot 180 ^{\circ} \\ m \angle ACZ= 90 ^{\circ} $$
Problem 6
$$ \overparen{MNJ} : \overparen {JLM}$$ is 3:2, what is the $$ m\angle MJK $$?
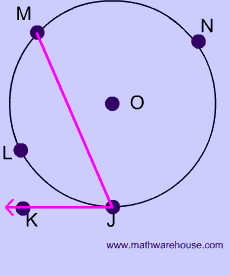
The key to this problem is recognizing that the total degrees in a circle is $$ 360^{\circ} $$ .
From there you can set up an equation using the 3:2 ratio.
$$ 3x + 2x =360 \\ 5x = 360 \\ \frac{5x}{5} = \frac{360}{5} \\ x = 72 \\ \overparen {JLM }= 2x = 2 \cdot 72 \\ \overparen {JLM }=144 ^{\circ} $$
At this point, you can use the formula, $$ \\ m \angle MJK= \frac{1}{2} \cdot 144 ^{\circ} \\ m \angle MJK = 72 ^{\circ} $$