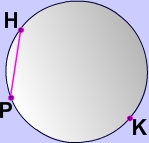
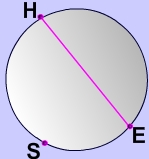
What is a Chord?
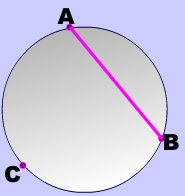
Answer: : A chord is a line segment that joins any two points on a circle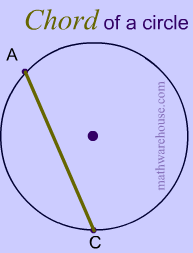
In other words, a chord is basically any line segment starting one one side of a circle, like point A in diagram 2 below, and ending on another side of the circle, like point B. Points A and B are the endpoints of chord AB.
Chord AB divides the circle into two distinct arcs from A directly to B and then the longer part: from A through C and to B.
Can you categorize these two arcs as the minor and major arc?