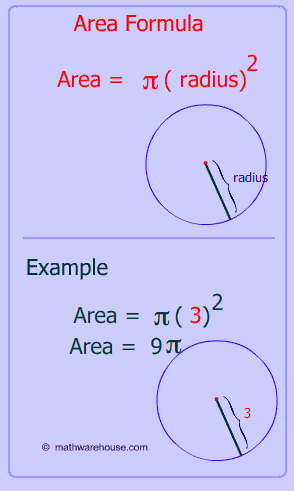
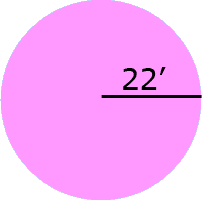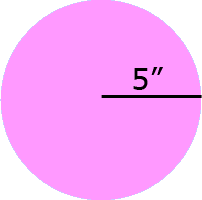Area of circle, formula and illustrated lesson: how to calculate the area of a circle

Formula for Area of circle

The formula to find a circle's area $$ \pi $$ (radius)² usually expressed as $$ \pi \cdot r^2 $$ where r is the radius of a circle.

Diagram 1

Area of Circle Concept

The area of a circle is all the space inside a circle's circumference. In diagram 1, the area of the circle is indicated by the blue color.

The area is not actually part of the circle. Remember a circle is just a locus of points. The area is enclosed inside that locus of points.

Interesting Fact about Circumference and Area

More interesting math facts here!

Explore and discover the relationship between the area formula, the radius of a circle and its graph with our interactive applet.

Practice Problems

Problem 1

What is the area of the circle in the picture?

Round your answer to the nearest tenth.

Remember the Formula:

$$ Area = \pi \cdot r^2 \\ A = \pi \cdot (22')^2 \\ A = \pi \cdot 484 \\ A = 1520.53084433746 \text{ square feet} \\ \\ Area = \boxed{1520.5} \\ \text {Rounded to nearest tenth} $$

Problem 2

What is this circle's area?

Round your answer to the nearest tenth.

Remember the Formula:

$$ Area = \pi \cdot r^2 \\ A = \pi \cdot (5")^2 \\ A = \pi \cdot 25 \text{ square inches} \\ A = 78.53981633974483 \text{ square inches} \\ A = 78.5 \\ \text{ square inches, rounded to nearest tenth} $$

Problem 3

What is the area of a circle with a radius of 7 centimeters?

Round your answer to the nearest hundredth.

Remember the Formula:

$$ Area = \pi \cdot r^2 \\ A = \pi \cdot (7 \text{ centimeters})^2 \\ A = 153.93804002589985 \text{ square centimeters} \\ \boxed {A = 153.94} \\ \text{ square centimeters, rounded to nearest hundredth} $$

Problem 4

What is the radius of a circle if its area is 120 in²? (Round your answer to the nearest hundredth of an inch)

Use the area formula ... but this time solve the radius.

$$ A = \pi r^2 \\ 120 = \pi r^2 \\ \frac{120}{\pi} = r^2 \\ 38.197 = r^2 \\ \sqrt{38.197} = r \\ \boxed {r=6.18 \text{ inches}} $$

Problem 5

What is the diameter of a circle if its area is 360 in²?

(Round your answer to the nearest hundredth of an inch)

Like the last problem, we are given area and need to solve for radius; However, this time, we need to then do one more step - find the diameter.

$$ A = \pi r^2 \\ 360 in^2= \pi r^2 \\ \frac{360}{\pi} = r^2 \\ 114.59155902616465= r^2 \\ \sqrt{114.59155902616465} = r \\ r=10.704744696916627 \text{ inches} \\ $$

Now, that we have found the radius, how do we find the diameter?

$$ diameter = 2 \cdot radius \\ = 2 \cdot 10.704744696916627 \\ =21.409489393833255 \\ \boxed{diameter =21.41} \\ \text{inches, rounded to nearest hundredth} $$

Challenge Problems

A circle has a diameter of 12 inches. What is its area in terms of $$ \pi $$.

(Need a hint)

Divide Diameter in half to calculate radius:

Radius = $$ \frac{diameter}{2} = \frac{12}{2}= 6 $$.

Use area formula:

$$ A= \pi \cdot r^2 \\ A = \pi \cdot 6^2 \\ A = 36 \pi $$

Problem 7

If a circle's radius is doubled, then how much did its area increase?

Since the formula for the area of a circle squares the radius, the area of the larger circle is always 4 (or 2²) times the smaller circle. Think about it: You are doubling a number (which means ×2) and then squaring this (ie squaring 2) -- which leads to a new area that is four times the smaller one.

You can see this relationship is true if you pick some actual values for the radius of a circle.

For instance, let's make the original radius = 3 .