Interactive Applet (html5)
$$
$$
Reset
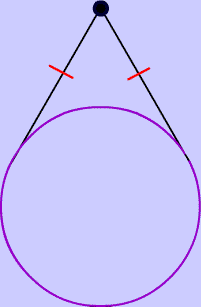
Two tangents from a common point are congruent!
The interactive applet below will show you this rule. Just drag the points around the screen and you'll see that--no matter what--the lengths of the tangents, are always equal.
Practice Problems
Problem 1
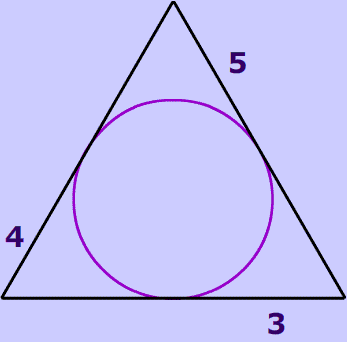
(Drawing not to scale)
Each side length that you know (5, 3, 4) is equal to the side lengths in red because they are tangent from a common point.
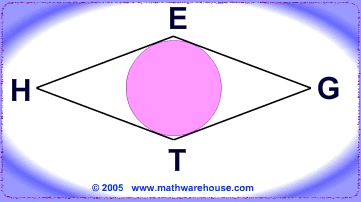
Problem 2
$$ EG = 10 \\ EH = 10 $$
- Find the following:
- A) GT
- B) HT
- C) Perimeter of quadrilateral EGTH.
Since two tangents from a common point (G and H) are congruent, $$ GT = EG = 10 $$, $$ HT = HE = 10 $$.
Perimeter of quadrilateral = 10 + 10 + 10 + 10 = 40.
What kind of quadrilateral is EGHT?
Since all four sides are congruent, it is a rhombus.
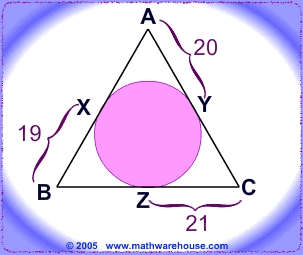
Problem 3
Related Pages:
