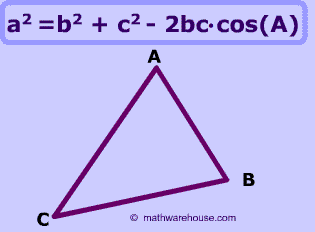Law of Cosines Formula
The law of cosines is a formula that relates the three sides of a triangle to the cosine of a given angle
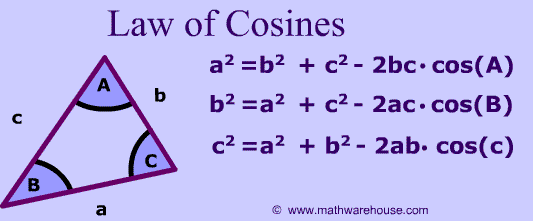
When to use law of cosines?
There are 2 cases for using the law of cosines.| What You Know | What You Can Find | |
|---|---|---|
|
Case I
2 sides and the included angle |
3rd side | |
|
Case II
3 Sides of Triangle |
Any Angle |
Why only the 'included' angle?
As you can see in the prior picture, Case I states that we must know the included angle . Let's examine if that's really necessary or not.
Interactive Demonstration of the Law of Cosines Formula
The interactive demonstration below illustrates the Law of cosines formula in action. Drag around the points in the triangle to observe who the formula works. Try clicking the "Right Triangle" checkbox to explore how this formula relates to the pythagorean theorem. (Applet on its own )
| a | b | c | |
|---|---|---|---|
| Length | 12.23 | 12.23 | 12.23 |
| Length2 | 12.23 | 12.23 | 12.23 |
Examples
Example 1
Given : 2 sides and 1 angle
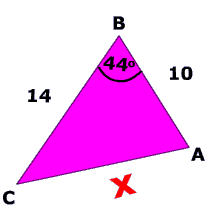
$$ b^2 = a^2 + c^2 - 2ac\cdot \text{cos}(44) \\ \red x^2 = 14^2 + 10^2 -2 \cdot 14 \cdot 10 \text{cos}(44 ^ \circ ) \\ \red x^2 = 14^2 + 10^2 -2 \cdot 14 \cdot 10 \text{cos}(44 ^ \circ ) \\ \red x^2 = 296 -280 \text{cos}(44 ^ \circ) \\ \red x^2 = 94.5848559051777 \\ \red x = \sqrt{ 94.5848559051777} \\ \red x = 9.725474585087234 $$
Example 2
Given : 3 sides
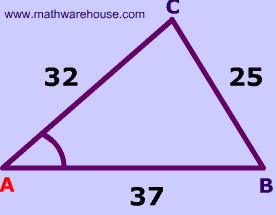
$$ a^2 = b^2 + c^2 - 2bc\cdot \text{cos}(\red A) \\ 25^2 = 32^2 + 37^2 -2 \cdot 32 \cdot 37 \cdot \text{cos}(\red A) \\ 625 =2393 - 2368\cdot \text{cos}(\red A) \\ \frac{625-2393}{ - 2368}= cos(\red A) \\ 0.7466216216216216 = cos(\red A ) \\ \red A = cos^{-1} (0.7466216216216216 ) \\ \red A = 41.70142633732469 ^ \circ $$
Practice Problem
The problems below are ones that ask you to apply the formula to solve straight forward questions. If they start to seem too easy, try our more challenging problems.
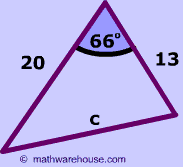
Problem 1
Use the law of cosines formula to calculate the length of side C.
$$ c^2 = a^2 + b^2 - 2ab\cdot \text{cos}( 66 ^\circ) \\ c^2 = 20^2 + 13^2 - 2\cdot20\cdot 13 \cdot \text{cos}( 66 ^\circ) \\ c^2 = 20^2 + 13^2 - 2\cdot20\cdot 13 \cdot \text{cos}( 66 ^\circ) \\ c^2 =357.4969456005839 \\ c = \sqrt{357.4969456005839} \\ c = 18.907589629579544 $$
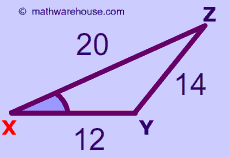
Problem 2
Use the law of cosines formula to calculate the measure of $$ \angle x $$
$$ a^2 = b^2 + c^2 - 2bc\cdot \text{cos}(A) \\ x^2 = y^2 + z^2 - 2yz\cdot \text{cos}(X ) \\ 14^2 = 20^2 + 12^2 - 2 \cdot 20 \cdot 12 \cdot \text{cos}(X ) \\ 196 = 544-480\cdot \text{cos}(X ) \\ \frac{196 -544}{480 } =\text{cos}(X ) \\ 0.725 =\text{cos}(X ) \\ X = cos^{-1}(0.725 ) \\ X = 43.531152167372454 $$
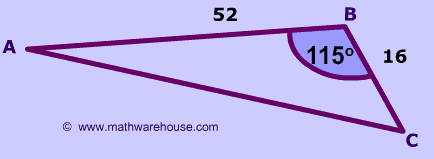
Problem 3
Use the law of cosines formula to calculate the length of side b.
$$ b^2= a^2 + c^2 - 2ac \cdot \text{cos}(115^\circ) \\ b^2= 16^2 + 5^2 - 2 \cdot 16 \cdot 5\text{ cos}( 115^\circ) \\ b^2 = 294.523784375712 \\ b = \sqrt{294.523784375712} \\ b =17.1616952652036098 \\ $$
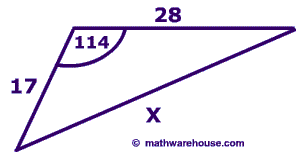
Problem 4
Use the law of cosines formula to calculate X.
$$ x^2 = 17^2 + 28^2 - 2 \cdot 17 \cdot 28 \text{ cos}(114 ^\circ) \\ x^2 = 1460.213284208162 \\ x =\sqrt{ 1460.213284208162} \\ x= 38.21273719858552 $$
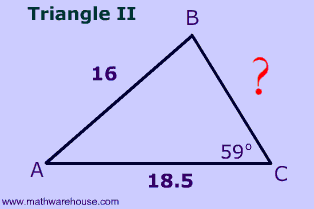
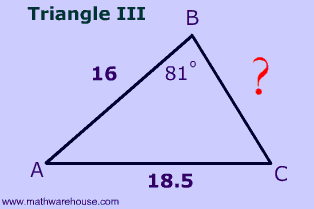
Problem 5
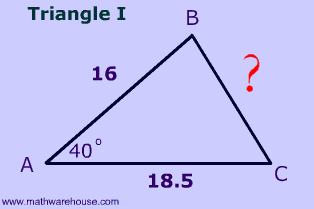
$$ \fbox{ Triangle 1 } \\ \red a^2 = b^2 + c^2 - 2bc \cdot cos (A) \\ \red a^2 = 18.5^2 + 16^2 - 2\cdot 18.5 \cdot 16 \cdot cos (44 ^\circ) \\ \red a^2 = 144.751689673565 \\ \red a = \sqrt{ 144.751689673565} = 12.031279635748021 $$
$$ \fbox{ Triangle 2 } \\ \red a^2 = b^2 + c^2 - 2bc \cdot cos (A) \\ \red a^2 = 18.5^2 + 16^2 - 2\cdot 18.5 \cdot 16 \cdot cos (\color{red}{A}) $$
Since we don't know the included angle, $$ \angle A $$, our formula does not help--we end up with 1 equation and 2 unknowns.
$$ \fbox{ Triangle 3 } \\ \red a^2 = b^2 + c^2 - 2bc \cdot cos (A) \\ \red a^2 = 18.5^2 + 16^2 - 2\cdot 18.5 \cdot 16 \cdot cos (\red A) $$
Since we don't know the included angle, $$ \angle A $$, our formula does not help--we end up with 1 equation and 2 unknowns.
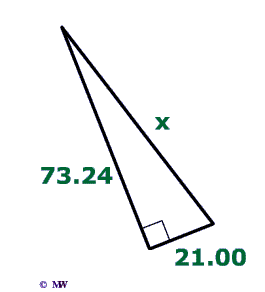
Problem 6
The value of x in the triangle below can be found by using either the Law of Cosines or the Pythagorean theorem. What conclusions can you draw about the relationship of these two formulas?
$$ \fbox{Law of Cosines} \\ x^2 = 73.24^2 + 21^2 - 2 \cdot 73.24 \cdot 21 \text{ cos}(90 ^\circ) \\ \text{remember : }\red{ \text{cos}(90 ^\circ) =0} \\ x^2 = 73.24^2 + 21^2 - 2 \cdot 73.24 \cdot 21 \cdot \red 0 \\ x^2 = 73.24^2 + 21^2 - \red 0 \\ x^2 = 73.24^2 + 21^2 \\ \fbox{Pytagorean Theorem} \\ a^2 = b^2 + c^2 \\ a^2 = 73.24^2 + 21^2 $$
As you can see, the Pythagorean theorem is consistent with the law of cosines. It turns out the Pythagorean theorem is just a special case of the law of cosines.
- Law of Cosines challenge problems (more advanced problems and also word problems)
- Law of cosines worksheet
- Law of sines vs cosines
- Pictures of law of sines and cosines
- Worksheet on law of sines and law of cosines (pdf)
