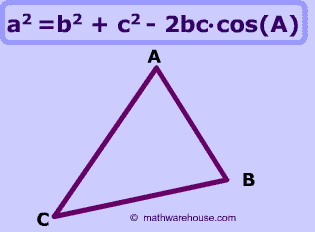This page assumes that you have a basic understanding of how to use law of cosines formula, and this page focuses solely on the law of cosines (no law of sines problems on this page)
Practice Problems
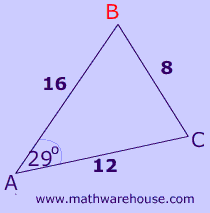
Problem 1
Use the law of cosines to calculate the measure of $$\angle B $$
Don't let the $$ 29 ^{\circ }$$ angle fool you.
Remember: you can only use an angle when you are trying to solve for the 3rd side of a triangle! The $$ 29^ \circ $$ does nothing for the law of cosines. (As an aside, you could use that angle with the law of sines .) You can even cross it out , if you want.
Step 1Since we want to find the value of $$ \angle B$$, we need
$$ b^2 = a^2 + c^2 -2ac \cdot cos( {\color{red}{B}} ) \\ $$
Substitute the values into the formula
$$ b^2 = a^2 + c^2 -2ac \cdot cos( {\color{red}{B}} ) \\ 12^2 = 8^2 + 16^2 -2\cdot 8 \cdot 16 \cdot cos( {\color{red}{B}} ) $$
Solve
$$ 12^2 = 8^2 + 16^2 -2\cdot 8 \cdot 16 \cdot cos( {\color{red}{B}} ) \\ 144= 320 - 256 cos( {\color{red}{B}}) \\ \frac{144 -320}{-256} = cos( {\color{red}{B}}) \\ 0.6875 = cos( {\color{red}{B}}) \\ {\color{red}{B}} = cos^{-1}(0.6875) \\ {\color{red}{B}} = 46.56746344221023 ^ \circ $$
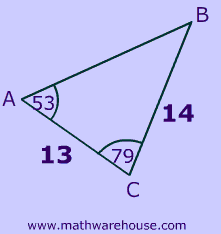
Problem 2
Use the law of cosines to find the length of side C
Don't let the $$ 53 ^{\circ}$$ angle fool you.
Remember: the law of cosines requires the use of the included angle. The $$ 53^ \circ $$ does nothing for you. ( Unless you know the law of sines.) You can even cross it out , if you want.
Step 1Determine the appropriate form of formula
Since we want to find side c we need
$$
{\color{red}{c}}^2 = a^2 + b^2 -2ab \cdot cos(C)
\\
$$
Substitute the values into the formula
$$ {\color{red}{c}}^2 = a^2 + b^2 -2ab \cdot cos( C) \\ {\color{red}{c}}^2 = 14^2 + 13^2 -2\cdot 14 \cdot 13 \cdot cos( 79) $$
Solve
$$ {\color{red}{c}}^2 = 14^2 + 13^2 -2\cdot 14 \cdot 13 \cdot cos( 79) \\ {\color{red}{c}}^2 = 295.5455256829377 \\ {\color{red}{c}} = \sqrt{ 295.5455256829377 } \\ {\color{red}{c}} = 17.191437568828782 $$
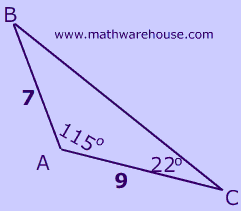
Problem 3
Use the law of cosines to find the length of side A
Don't let the $$ 22 ^{\circ}$$ angle fool you.
Remember: you can only use an angle when you are trying to solve for the 3rd side of a triangle! The $$ 22^ \circ $$ does nothing for you. ( Unless you know the law of sines.) You can even cross it out , if you want.
Step 1Determine the appropriate form of formula
Since we want to find side c we need
$$
{\color{red}{a}}^2 = b^2 + c^2 -2bc \cdot cos( A )
$$
Substitute the values into the formula
$$ {\color{red}{a}}^2 = b^2 + c^2 -2bc \cdot cos( A ) \\ {\color{red}{a}}^2 = 9^2 + 7^2 -2 \cdot 9 \cdot 7 \cdot cos( 115 ) \\ $$
Solve
$$ {\color{red}{a}}^2 = 9^2 + 7^2 -2 \cdot 9 \cdot 7 \cdot cos( 115 ) \\ {\color{red}{a}}^2 = 171.05203545771545 \\ {\color{red}{a}} = \sqrt{ 171.05203545771545 } \\ {\color{red}{a}} = 13.07868630473701 $$
Word Problems
Problem 4
For word problems, the best thing to do , first and foremost, is draw a diagram.
Step 1Draw picture
There are actually many ways to draw this triangle, but one version of the diagram is:
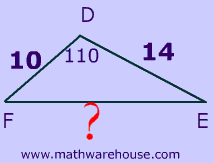
Regardless of how you draw it, the $$ 110^ \circ $$ degree angle should be in between the two known sides
Set up formula and substitute the values
$$ a^2 = b^2 + c^2 -2bc \cdot cos( A ) \\ {\color{red}{d}}^2 = e^2 + f^2 -2ef \cdot cos( D ) \\ {\color{red}{d}}^2 = 10^2 + 14^2 -2 \cdot 10 \cdot 14 \cdot cos( 110 ) \\ $$
Solve and round
$$ {\color{red}{d}}^2 = 200.23435986881276 \\ {\color{red}{d}} = \sqrt{200.23435986881276} \\ {\color{red}{d}} = 14.15041907043084 \\ {\color{red}{d}} = 14.2 $$
Problem 5
For word problems, the best thing to do , first and foremost, is draw a diagram.
Step 1Draw picture
There are actually many ways to draw this triangle, but one version of the diagram is:
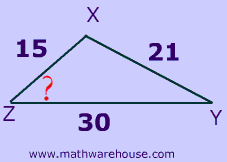
Set up formula and substitute the values
$$ a^2 = b^2 + c^2 -2bc \cdot cos( A ) \\ z ^2 = x^2 + y^2 -2xy \cdot cos( {\color{red}{ Z}} ) \\ 21 ^2 = 30^2 + 15^2 -2 \cdot 30 \cdot 15 \cdot cos( {\color{red}{ Z }} ) $$
Solve and round
$$ 441 = 1125 - 900 \cdot cos( {\color{red}{ Z }} ) \\ \frac{441 - 1125}{ - 900 } = cos( {\color{red}{ Z }} ) \\ 0.76 = cos( {\color{red}{ Z }} ) \\ {\color{red}{ Z }} = cos^{-1}(.76) \\ {\color{red}{Z}} = 40.535802111316556 \\ {\color{red}{Z}} = 40.54 $$
Problem 6
For word problems, the best thing to do, first and foremost, is draw a diagram.
Step 1Draw picture
There are actually many ways to draw this triangle, but one version of the diagram is:
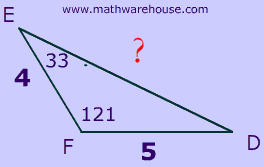
Note, you only need one of the two angles. Can you tell which one? Click to cross out the unneeded angle
Set up formula and substitute the values
$$ a^2 = b^2 + c^2 -2bc \cdot cos( A ) \\ {\color{red}{f}} ^2 = d^2 + e^2 -2de \cdot cos( F ) \\ {\color{red}{f}} ^2 = 4^2 + 5^2 -2\cdot 4 \cdot 5 \cdot cos( 121 ^\circ ) $$
Solve and round
$$ {\color{red}{f}} ^2 = 4^2 + 5^2 -2\cdot 4 \cdot 5 \cdot cos( 121 ^\circ ) \\ {\color{red}{f}} ^2 = 61.60152299640217 \\ {\color{red}{f}} = \sqrt{61.60152299640217} \\ {\color{red}{f}} = 7.8486637713946035 \\ {\color{red}{f}} = 7.849 $$
