When to Use Law of Sines vs Cosines?
The goal of this page is to help students better understand when to use the Law of Sines and when to use the Law of Cosines
Practice Problems
Problem 1
Can you use the Law of Sines , the Law of Cosines , or neither to solve the unknown side in triangle 1 below?
Law of Sines
Just look at it. You can always immediately look at a triangle and tell whether or not you can use the Law of Sines.
You need either 2 sides and the non-included angle or, in this case, 2 angles and the non-included side.
The law of sines is all about opposite pairs.
In this case, we have a side of length 11 opposite a known angle of $$ 29^{\circ} $$ (first opposite pair) and we want to find the side opposite the known angle of $$ 118^\circ$$.
First Step $ \frac{\red x} {sin(118^{\circ})} = \frac{11}{ sin(29^{\circ})} $
Problem 2
Can you use the Law of Sines , the Law of Cosines , or neither to solve the unknown side in the triangle below?
Law of Cosines
Remember, the law of cosines is all about included angle (or knowing 3 sides and wanting to find an angle).
In this case, we have a side of length 20 and of 13 and the included angle of $$ 66^\circ$$.
First Step $ \red a^2 = b^2 + c^2 - 2bc \cdot cos( \angle a ) \\ \red a^2 = 20^2 + 13^2 - 2\cdot 20 \cdot 13 \cdot cos( 66 ) $
Problem 3
Can you use the Law of Sines , the Law of Cosines , or neither to solve the unknown side triangle 1?
Law of Sines
Just look at it. You can always immediately look at a triangle and tell whether or not you can use the Law of Sines.
You need either 2 sides and the non-included angle (like this triangle) or 2 angles and the non-included side.
Remember, the law of sines is all about opposite pairs.
In this case, we have a side of length 16 opposite a known angle of $$ 115^{\circ} $$ (first opposite pair) and we want to find the angle opposite the known side of length 32 . We can set up the proportion below and solve :
First Step $ \frac{sin(115^{\circ})}{16} = \frac{sin(\red x)}{32} $
Problem 4
Decide which formula (Law of Sines/Cosines) you would use to calculate the value of $$ \red x$$ below? After you decide that, try to set up the equation (Do not solve -- just substitute into the proper formula).
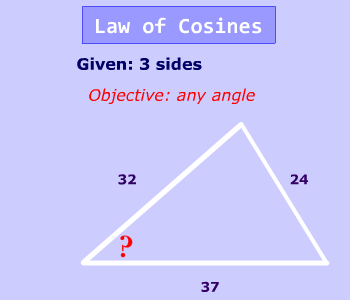
Law of Cosines
Since you know 3 sides, and are trying to find an angle this is Law of Cosines problem.
First Step $ 8^2 = 5^2 + 6^2 -2(5)(6) \cdot cos( \red x) $
Problem 5
Decide which formula (Law of Sines/Cosines) you would use to calculate the value of $$ \red x $$ below? After you decide that, try to set up the equation (Do not solve -- just substitute into the proper formula).
Law of Cosines
Since you know 2 sides, their included angle, and you are trying to find the side length opposite the angle, this is Law of Cosines problem.
First Step $ \red x^2 = 11^2 + 7^2 -2(11)(7) \cdot cos(50) $
Problem 6
Decide which formula (Law of Sines/Cosines) you would use to calculate the value of x below? After you decide that, try to set up the equation (Do not solve -- just substitute into the proper formula).
Law of Sines
Just look at it. You can always immediately look at a triangle and tell whether or not you can use the Law of Sines.
You need either 2 sides and the non-included angle (like this triangle) or 2 angles and the non-included side.
Since you know a side length (11) and its opposite angle (50) and want to calculate the angle measurement opposite the length of side 7, this is a Law of Sines problem
First Step $ \frac{sin ( \red x)} {7 } = \frac{sin(50)}{11} $
