What are the remote and interior angles?
It's all about extending a side of the triangleAn exterior angle of a triangle, or any polygon, is formed by extending one of the sides.
In a triangle, each exterior angle has two remote interior angles . The remote interior angles are just the two angles that are inside the triangle and opposite from the exterior angle.
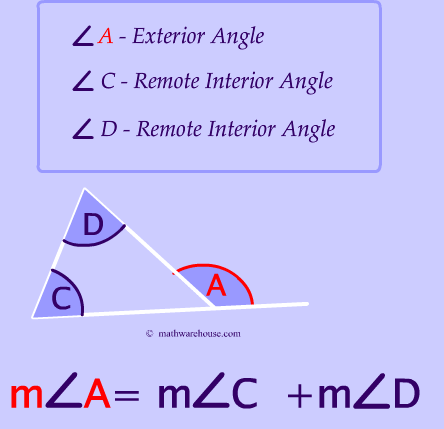
As the picture above shows, the formula for remote and interior angles states that the measure of a an exterior angle $$ \angle A $$ equals the sum of the remote interior angles.
To rephrase it, the angle 'outside the triangle' (exterior angle A) equals D + C (the sum of the remote interior angles).
Interactive Demonstration of Remote and Exterior Angles
The interactive program below allows you to drag the points of the triangle around. Notice that the sum of the remote interior angles (C and D) equal the measure of exterior angle A.
Practice Problems
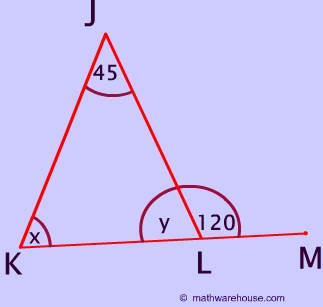
Problem 1
Use the formulas described on this page to calculate the values of x (a remote interior angle) and of Y.
Since X and, $$ \angle J $$ are remote interior angles in relation to the 120° angle, you can use the formula.
$$ 120° = 45° + x \\ 120° - 45° = x \\ 75° = x. $$
Now, since the sum of all interior angles of a triangle is 180°. You can solve for Y.
$$ 75° + 45° + y = 180° \\ 120° + Y = 180° \\ Y = 60° $$
