How do we prove triangles are similar?
Answer: Use any of the 3 theorems : AA, SAS, SSS
I. AA Theorem
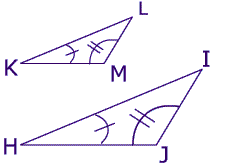
When 2 angles of one triangle are equal to 2 corresponding angles of the other triangle,the two triangles must be similar.
III. SSS Theorem
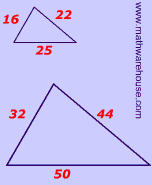
If three pairs of corresponding sides are proportional, then the triangles must be similar. Be careful - don't confuse this with the SSS theorem for proving triangles congruent. Similar triangles are about proportional sides.
II. SAS Theorem
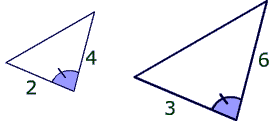
If two sides and the included angle of one triangle are in the same ratio as the corresponding two sides and included angle in another triangle, then the triangles must be similar.
When 2 angles of one triangle are equal to 2 corresponding angles of the other triangle,the two triangles must be similar.
Practice Problems
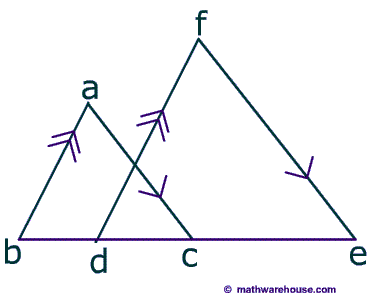
Yes, the parallel lines give you two pairs of corresponding congruent angles so you can use the AA Theorem.
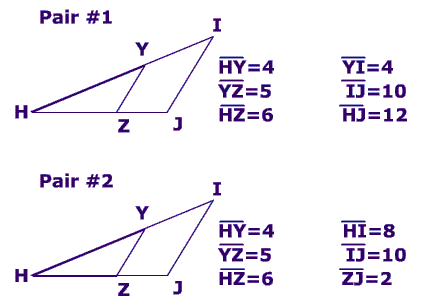
The SSS theorem requires that 3 pairs of sides that are proportional.
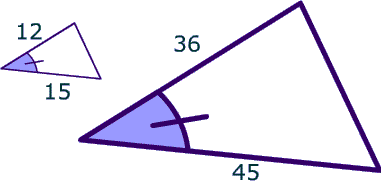
In pair 1, all 3 sides have a ratio of $$ \frac{1}{2} $$ so the triangles are similar.
In pair 2, two pairs of sides have a ratio of $$ \frac{1}{2}$$ , but the ratio of $$ \frac{HZ}{HJ} $$ is the problem.
First off, you need to realize that ZJ is only part of the triangle side, and that HJ = 6 + 2 =8 .
Once you recognize that, you can look at the ratio $$ \frac{HZ}{HJ} $$ :
$ \frac{6}{6+2} \\ \frac{6}{8} \\ \frac{3}{4} $
And since these side lengths do not have the same proportion as the other two pairs, they are not similar by SSS.
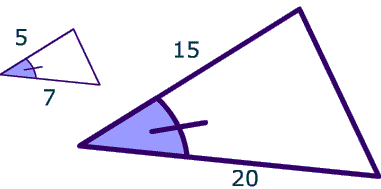
Yes, since two pairs of corresponding sides have a $$ \frac{1}{3} $$ ratio and the included angle is congruent, these two triangles are similar by the Side Angle Side theorem.
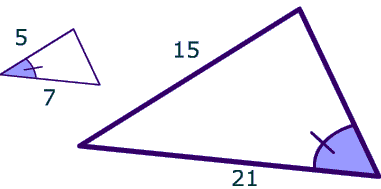
No, although the included angle is equal, the sides do not have a constant ratio $$ \frac{5}{15} $$ and $$ \frac{7}{20} $$.
No, although we have 2 pairs of sides with an the same $$ \frac{1}{3} $$ ratio, we do not have the included angle so we can not state that the triangles are similar.