What are corresponding sides and angles?
Corresponding sides and angles are a pair of matching angles or sides that are in the same spot in two different shapes. Look at the pictures below to see what corresponding sides and angles look like.
Note:Angles, sides in the same 'spot'
Corresponding sides and angles are a pair of matching angles or sides that are in the same spot in two different shapes. Look at the pictures below to see what corresponding sides and angles look like.
Note:
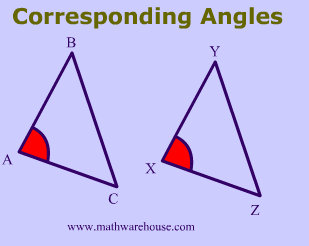
In $$\triangle \red{A}BC $$ and $$\triangle \red{X}YZ $$,
$$\angle A$$ corresponds with $$\angle X$$.
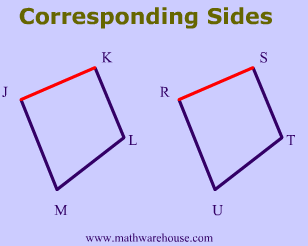
In quadrilaterals $$\red{JK}LM$$ and $$\red{RS}TU$$,
$$ \overline {JK} $$ corresponds with $$ \overline{RS} $$ .
In quadrilaterals $$ABC\red{D}E $$ and $$HIJ\red{K}L $$,
$$\angle D$$ corresponds with $$\angle K$$.
In quadrilaterals $$A\red{BC}DE $$ and $$H\red{IJ}KL $$,
$$ \overline {BC} $$ corresponds with $$ \overline {IJ} $$.
Orientation does not affect corresponding sides/angles. It only makes it harder for us to see which sides/angles correspond.
The two triangles below are congruent and their corresponding sides are color coded. Try pausing then rotating the left hand triangle. Notice that as the triangle moves around it's not always as easy to see which sides go with which. (Imagine if they were not color coded!).
If $$\triangle ABC $$ and $$ \triangle UYT$$ are similar triangles, then what sides/angles correspond with:
| AB |
Follow the letters the original shapes: $$\triangle \red{AB}C $$ and $$ \triangle \red{UY}T $$. Answer:UY |
| $$ \angle BCA $$ |
Follow the letters the original shapes: $$\triangle ABC $$ and $$ \triangle UYT $$. Answer: $$ \angle YTU $$ |
| TU |
Follow the letters the original shapes: $$\triangle\red{A}B\red{C} $$ and $$ \triangle \red{U} Y \red{T} $$. Answer: CA |
| $$ \angle TUY $$ |
Follow the letters the original shapes: $$\triangle ABC $$ and $$ \triangle UYT $$. Answer: $$ \angle CAB$$ |