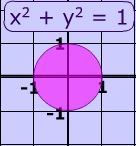
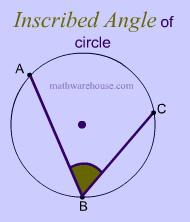
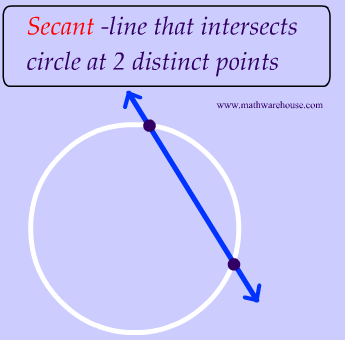
Circle Calculator
Invalid input
Status: Calculator waiting for input

$$ $$
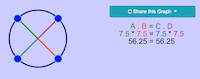
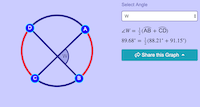
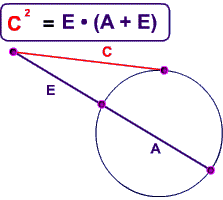
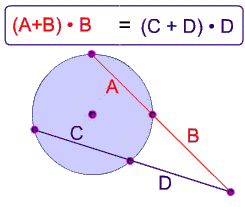
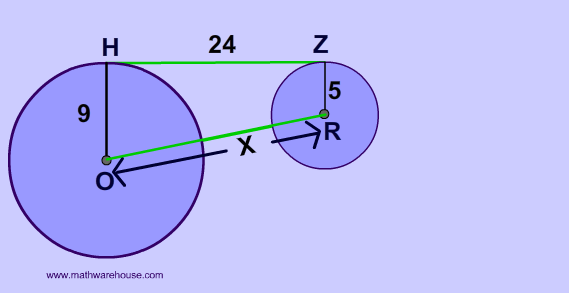
Power of the Point
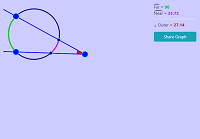
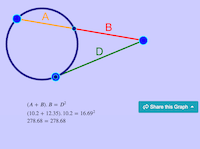
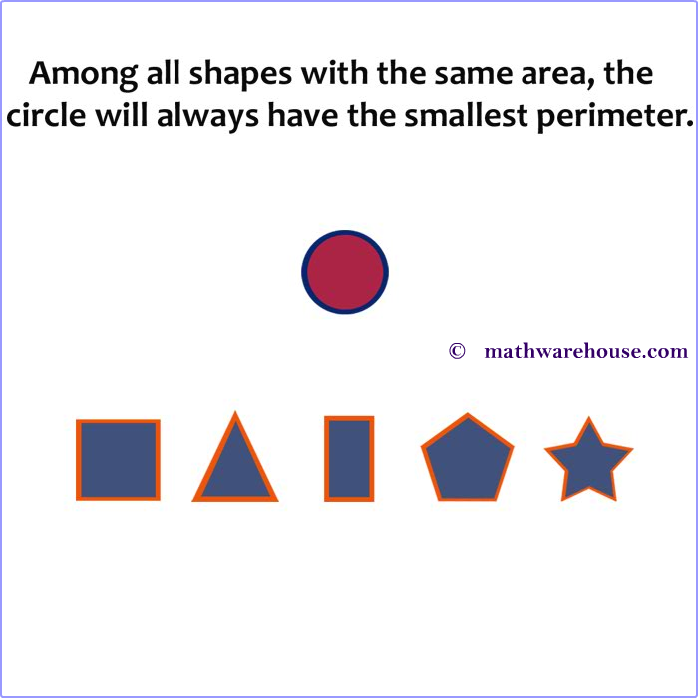
Interesting Fact about Circumference and Area
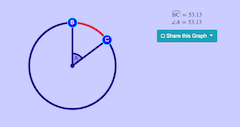
Big Circle Q
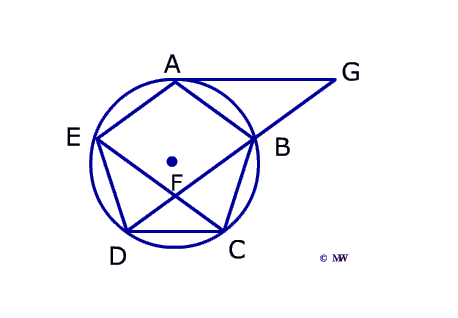
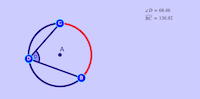
To solve this probelm, you must remember how to find the meaure of the interior angles of a regular polygon. In the case of a pentagon, the interior angles have a measure of (5-2) •180/5 = 108 °. Therefore, each inscribed angle creates an arc of 216°
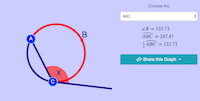
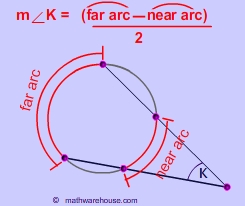
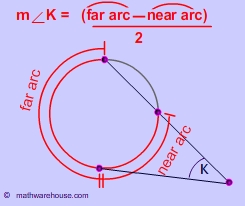
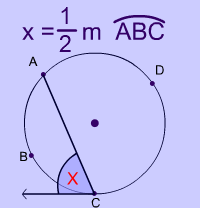
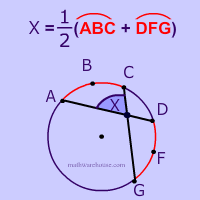
Use the inscribed angle formula and the formula for the angle of a tangent and a secant to arrive at the angles
-
m
 BDE = 72 °
BDE = 72 °
-
m
 BFC = 72 °
BFC = 72 °
-
m
 AGD = ½(144 −72) = 36 °
AGD = ½(144 −72) = 36 °