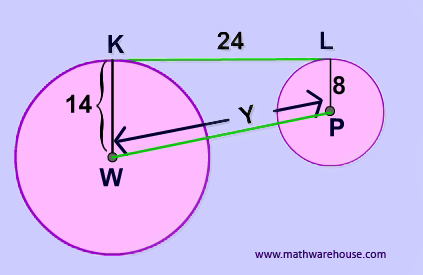
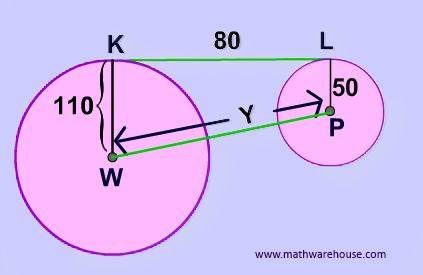
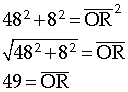Problem 1
Step 1
Create the rectangle.
Step 2
$
WP^2 = 6^2 + 24^2
\\
WP = \sqrt{ 6^2 + 24^2 }
\\
\text{m } \overline{WP} \approx 24.7
$