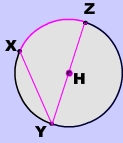
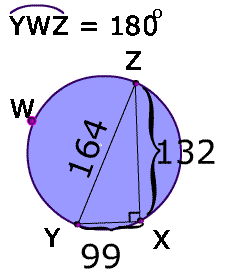What is an Inscribed Angle ?
Answer:Is formed by 3 points that all lie on the circle's circumference.
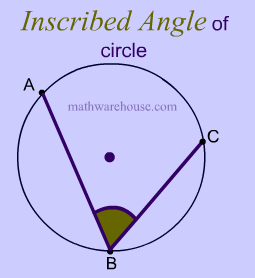
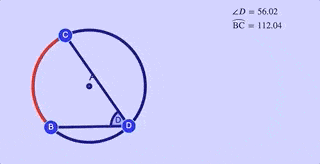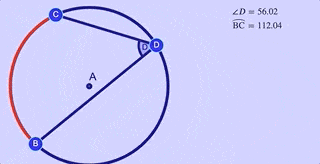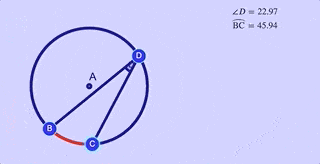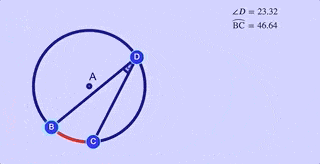
The measure of the inscribed angle is half of measure of the intercepted arc .
$ \text{m } \angle b = \frac 1 2 \overparen{AC} $
Explore this relationship in the interactive applet immediately below.
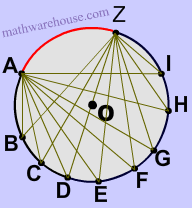
Every single inscribed angle in diagram 2 has the exact same measure, since each inscribed angle intercepts the exact same arc, which is $$ \overparen {AZ} $$.
Practice Problems
Problem 1
$$ \overparen{XZ}\text{ is the intercepted arc} \\ \angle{Y}\text{ is the inscribed angle} \\ $$
Follow Up Question
If $$ m\overparen{XZ} =40^{o} $$, what is the measure of inscribed angle $$ Y $$?
$ \red{ \text{m } \angle Y} = \frac 1 2 \overparen{XZ} \\ \red{ \text{m } \angle Y } = \frac 1 2 40 ^{\circ} \\ \red{ \text{m } \angle Y } = 20 ^{\circ} $
Problem 2
The error is that $$ 99^2 + 132^2 \ne 164^2 $$. Since the Pythagorean theorem does not hold, $$\angle X $$ is not a right angle and $$ \text{ m } \overparen{YWZ} \ne 180^{\circ}.$$