Tangent and Secant
![power of point tan secant]()
Two Secants
![power of point 2 secants sides]()
Note: For the special case of two tangents , please visit this page .
This page:
Interactive Applet
$$
B^{2} = D^{2}
\\
\class{data-line-A}{07.34}^{2}
= \class{data-line-C}{08.39}^{2}
\\
\class{data-line-f}{142.19} = \class{data-line-f}{142.19}
$$
$$
( A + B ) . B = D^{2}
\\
( \class{data-line-B}{12.02} + \class{data-line-A}{07.34} ) . \class{data-line-B}{07.34}
= \class{data-line-C}{08.39}^{2}
\\
\class{data-line-f}{142.19} = \class{data-line-f}{142.19}
$$
$$
B^{2} = ( C + D ) . D
\\
\class{data-line-A}{07.34}^{2}
= ( \class{data-line-D}{08.53} + \class{data-line-C}{08.39} ) . \class{data-line-C}{08.39}
\\
\class{data-line-f}{142.19} = \class{data-line-f}{142.19}
$$
$$
( A + B ) . B = ( C + D ) . D
\\
( \class{data-line-B}{12.02} + \class{data-line-A}{7.34} ) . \class{data-line-A}{7.34}
= ( \class{data-line-D}{8.53} + \class{data-line-C}{8.39} ) . \class{data-line-C}{8.39}
\\
\class{data-line-f}{142.19} = \class{data-line-f}{142.19}
$$
Drag Points To Start Demonstration
Practice Problems
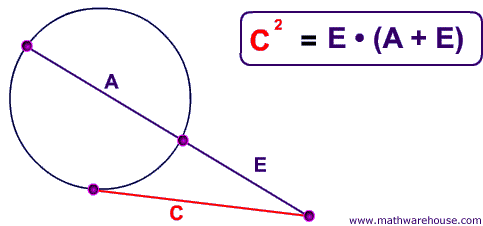
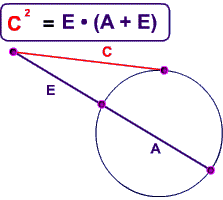
Use the theorem for the intersection of a tangent and a secant of a circle to solve the problems below.
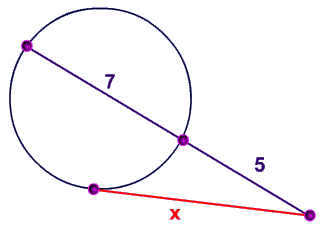
Problem 1
In this diagram, the red line is a tangent, how long is it?
$ \red x^2 = (7 + \blue 5) \cdot \blue 5 \\ \red x^2 = ( 12 ) \cdot \blue 5 \\ \red x^2 = 60 \\ \red x = \sqrt{60} $
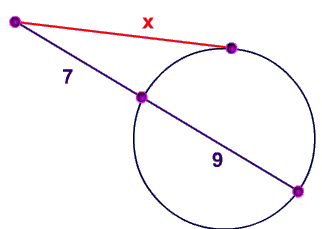
Problem 2
In the problem below, the red line is a tangent of the circle, what is its length?
$ \red x^2 = (9+ \blue 7) \cdot \blue 7 \\ \red x^2 = (16) \cdot \blue 7 \\ \red x^2 = 112 \\ \red x = \sqrt{ 112 } $
This page:
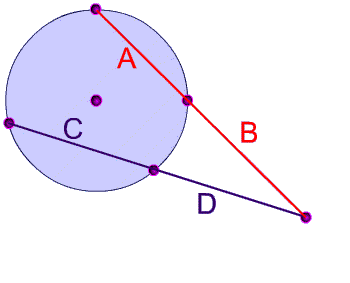
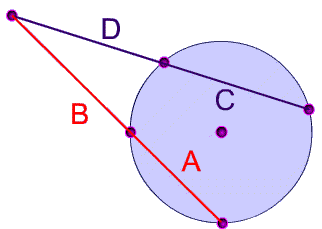
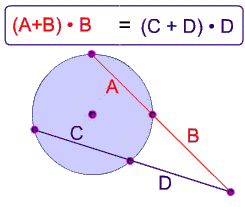
Two Secants Intersecting
Formula:
If two secant segments are drawn from a point outisde a circle, the product of the lengths (C + D) of one secant segment and its exteranal segment (D) equals the product of the lengths (A + B) of the other secant segment and its external segment (B).
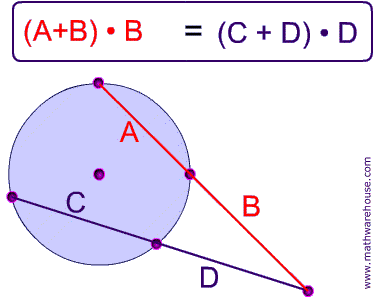
Problem 3
Use the theorem above to determine A if $$ B = 4, C = 8, D = 5 $$ .
$ (A + \blue 4) \cdot \blue 4 = (8 + \blue 5) \cdot \blue 5 \\ (A + \blue 4) \cdot \blue 4 = (14 ) \cdot \blue 5 \\ (A + \blue 4) \cdot \blue 4 = 65 \\ \frac 1 4 \cdot (A + \blue 4) \cdot \blue 4 =\frac 1 4 \cdot 65 \\ \frac {1}{ \cancel 4} \cdot (A + \blue 4) \cdot \blue {\cancel {4}} = 16.25 \\ A + \blue 4 - 4 = 16.25 - 4 \\ A = 12.25 $
Problem 4
Use the theorem above to determine A if $$ B = 8, C = 16, D = 10 $$.
$ (A + \blue 8) \cdot \blue 8 = (16 + \blue 10) \cdot \blue 10 \\ (A + \blue 8) \cdot \blue 8 = (26) \cdot \blue 10 \\ (A + \blue 8) \cdot \blue 8 = 260 \\ \frac1 8 \cdot (A + \blue 8) \cdot \blue 8 = \frac1 8 \cdot 260 \\ (A + \blue 8) = 32.5 \\ A = 32.5 - 8 \\ A = 24.5 $
Problem 5
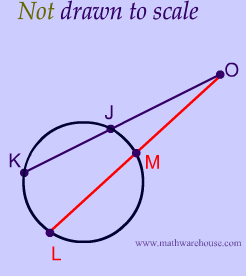
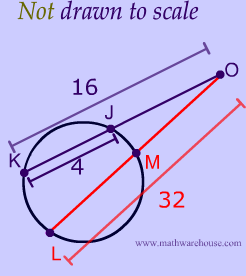
The two secants in the picture below are not drawn to scale. If $$ KO = 16$$, $$ KJ = 4 $$, and $$ LO = 32$$ , what is $$LM$$ ?
The first challenge here is for you to recognize that the side lengths we are given are not the ones that we can use for the formula!!. Please see the diagram below, which labels the measurements that we are given.:
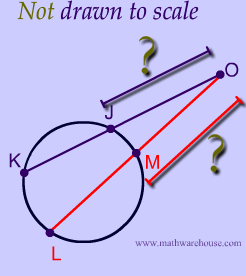
So, the first thing we must do is is figure out the portion of the secants that are outside the circle.
$
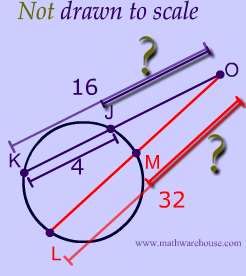\color{#666600}{ JO } = 16 - 4 = 12
\\
\text{Now, apply formula :}
\\
KO \cdot JO = LO \cdot MO
\\
16 \cdot 12 = 32 \cdot MO
\\
192 = 32 \cdot MO
\\
\frac{ 192}{32} = \frac{32}{32} \cdot MO
\\
6 = MO
\\
\text{Now, question asks for LM}
\\
LM = LO-MO
\\
LM = 32 - 6 = \boxed{ 26}
$
Related Pages:
