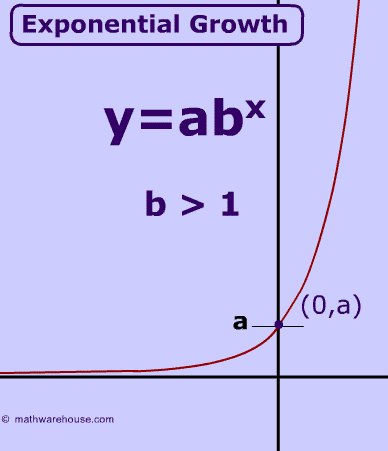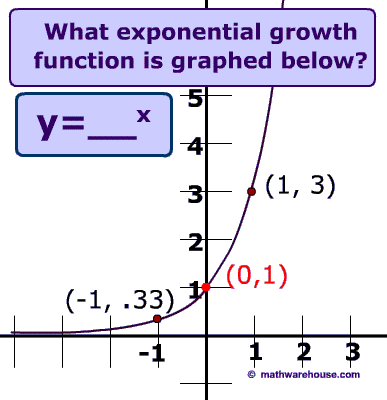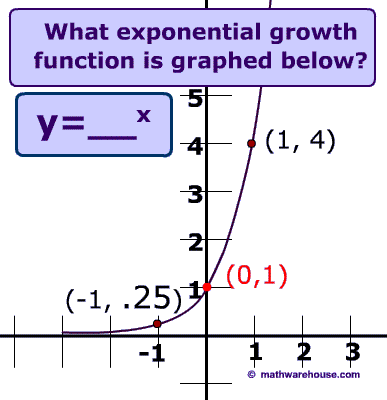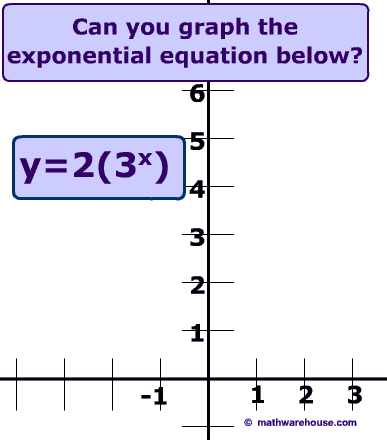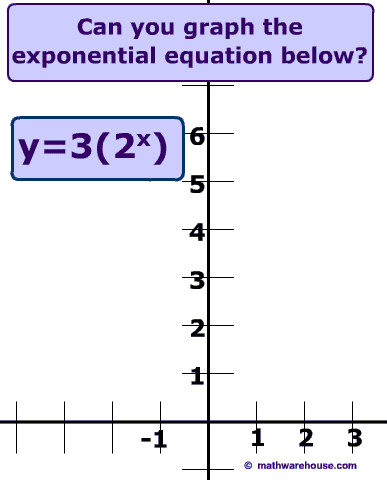Exponential Growth, its properties, how graph relates to the equation and formula--Visual Lesson

Properties

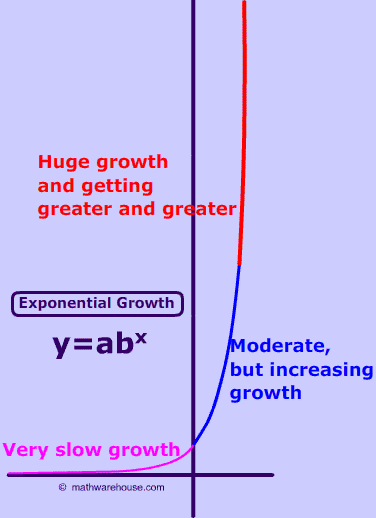
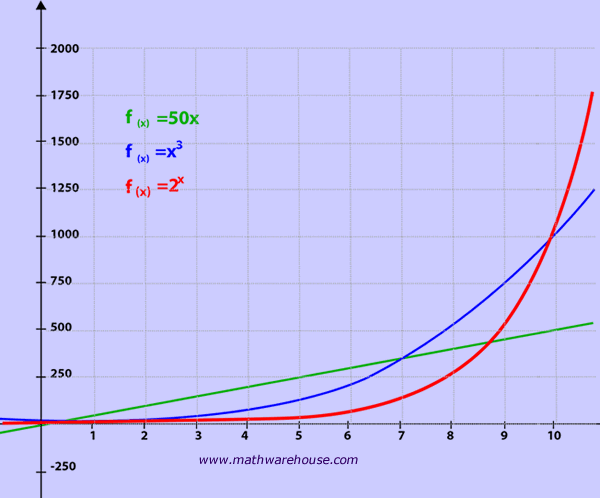
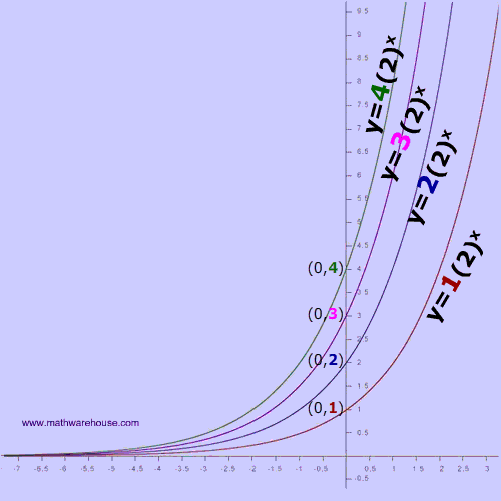
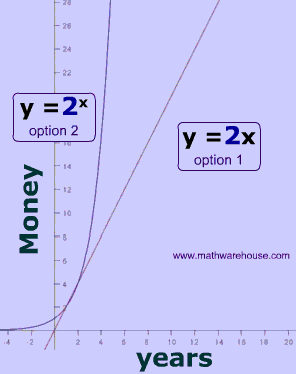
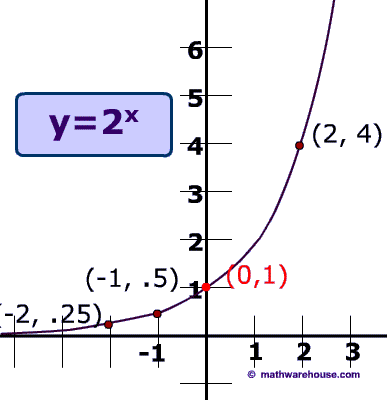
Property #1) rate of growth starts slow and increases (Read on, to learn more about this property, which is the primary focus of this web page)
Property #2) The domain is all real numbers. $$ \{x: x \in \mathbb{R}\} $$
Property #3)The range is all positive real numbers greater than 0 .$$ \{ y: y> 0 \} $$
Read more here
Property #4) It is a one-to-one function
Property #5) The graph is asymptotic with the a horizontal line. Read more about this
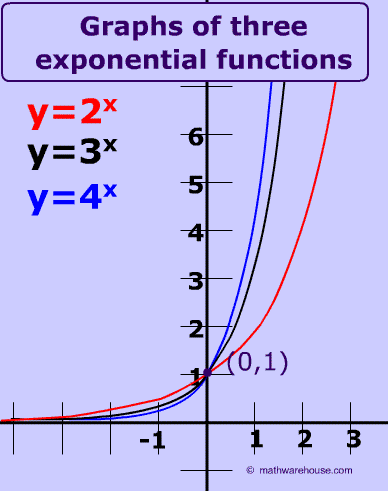
Property #6) The value of 'b' in the general equation must be
greater than 1
Property #7) The inverse of exponential growth is logarithmic functions.
Of note: Exponential decay is not the inverse of exponential growth.

How Equation relates to Graph

Graph 1

picture of formula for exponential graph equation and graph

In the general example shown in Graph 1, 'a' stands for the initial amount, and 'b' is any real number that is greater than 1.

The graph's asymptote at x -axis

When B is less than 1, you are not dealing with exponential growth but rather exponential decay (Lesson on Decay).

What about when b is exactly equal to 1?

In this case, you are not dealing with an exponential equation, but rather a linear equation. (Link) $ y = ab^x \\ y = a(1)^x \\ y = a $

As you can see from the work above, and the graph, when b is 1, you end up with the equation of a horizontal line ( Link ) .

The Graph

Graph 2

Property #1) Rate of growth of exponential growth increases more and more, until it becomes massive!

As Graph 2shows, at first, exponential growth does not increase much, but the rate of growth of begins increasing more and more until the rate of increase becomes massive.

Table of Values

The table of values for the exponential growth equation $$y = 9^x $$ demonstrates the same property-growth rate starts slow and soon gets massive

At first the rate of increase is small, but the pace increases and soon enough the rate of increase is massive.

Just look at the difference between x = 7 and x = 8, the value of the function increases by more than 38 MILLION!

How does this compare to other graphs/functions?

As the graph below shows, exponential growth

at first, has a lower rate of growth than the linear equation f(x) =50x
at first, has a slower rate of growth than a cubic function like f(x) = x³, but eventually the growth rate of an exponential function f(x) = 2^x , increases more and more -- until the exponential growth function has the greatest value and rate of growth!

Moral of the story: Exponential growth eventually grows at massive rates, even though it starts out growing slowly. This 'trend' is true and, when compared to other graphs, exponential growth eventually outpaces most other functions's rate of increase.