Mathwarehouse Logo

One to One Function

Range, Domain, horizontal line test

Worksheet On this Page

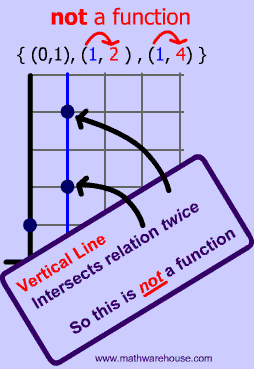
What is a 1 to 1 function?

A special type of function.

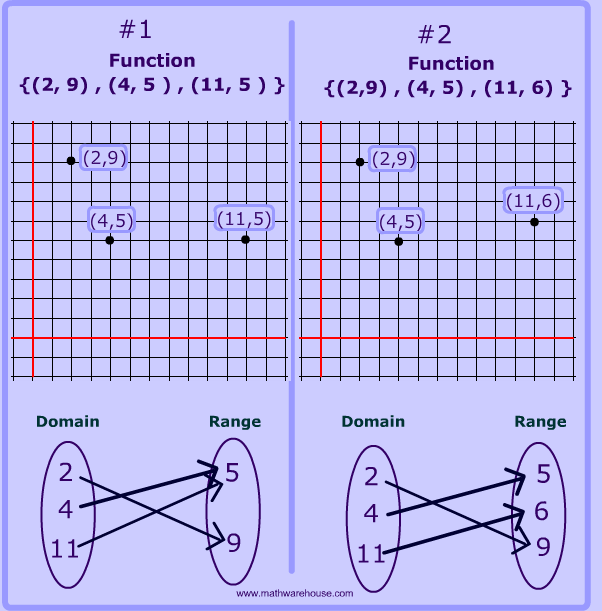
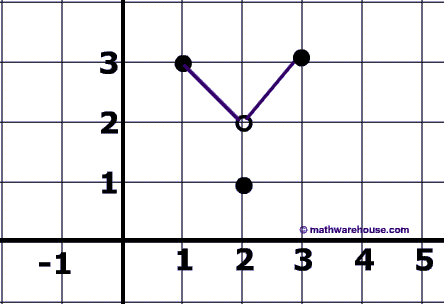
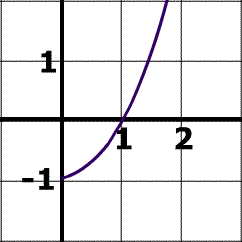
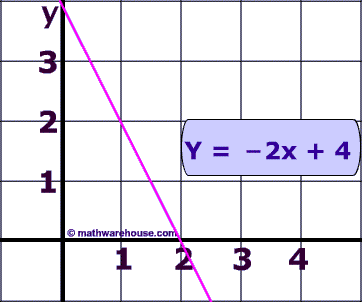
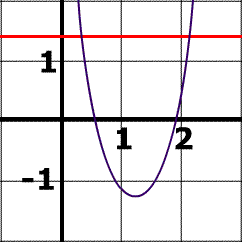
Look at the two functions below, (# 1 and #2). They only differ by a single number .

One of the functions is one to one , and the other is not.

Which function below is 1 to 1?

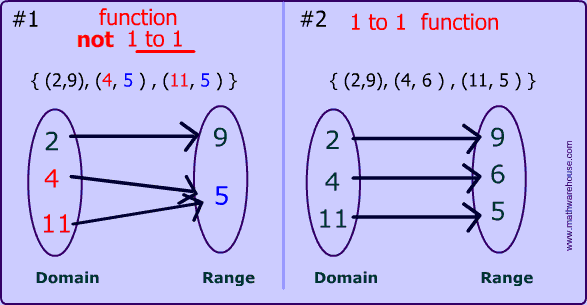
Function #2 on the right side is the one to one function . In a one to one function, every element in the range corresponds with one and only one element in the domain.

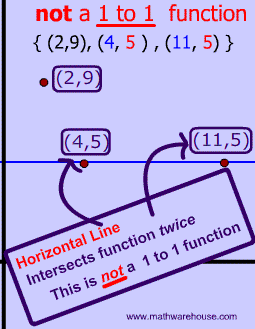
So, #1 is not one to one because the range element. 5 goes with 2 different values in the domain (4 and 11).

Diagram 1
example of one to graph, chart, example

How to know if $$ f(x) $$ is 1 to 1?

To be a function

Only one thing must be true : each element in domain must go to a unique range element. ( prior lesson)

Diagram 2
relation vs function set of points

To be a 1 to 1 function

Two things must be true.

First: It must be a standard function. In other words, it must satisfy requirements for function .

Second: This is the new part. each element in range must go to a unique element in the domain.

Diagram 3
One to One function points
So, there is one new characteristic that must be true for a function to be one to one. This new requirement can also be seen graphically when we plot functions, something we will look at below with the horizontal line test.

Horizontal Line Test

We can also look at the graphs of functions and use the horizontal line test to determine whether or not a function is one to one.

To be a function

Only one thing must be true : The relation must pass the vertical line test. ( link) . vetical line test picture

As we learned in our vertical line test lesson, this is really the exact same as saying "elements in the domain cannot repeat".

To be a 1 to 1 function

Two things must be true.

First: It must be a standard function. In other words, it must pass the vertical line test.

Second: This is the new part. It must also pass the horizontal line Test .

Picture of horizontal line test graph

Arrow Charts

Arrow Chart of 1 to 1 vs Regular Function

Below you can see an arrow chart diagram that illustrates the difference between a regular function and a one to one function.

Function #1 is not a 1 to 1 because the range element of '5' goes with two different elements (4 and 11) in the domain. .

one to one function arrow chart example

Practice Problems - Part I

Problem 1

Which functions below are 1 to 1?

  • Function #1 {(2, 27), (3, 28), (4, 29), (5, 30)}
  • Function #2 {(11,14), (12, 14), (16, 7), (18, 13)}
  • Function #3 {(3, 12), (4, 13), (6, 14), (8, 1)}

If an element in the range repeats, like 14 in function #2 , then you do not have a 1 to 1 function.

Relation #1 and Relation #3 are both one-to-one functions.

Problem 2

Which functions below are one to one?

  • Function #1 {(2, 1), (4, 5), (6, 7), (8, 9)}
  • Function #2 {(3,6), (8, 5), (6, 7), (22,6)}
  • Function #3 {(-3, 4), (21, -5), (0, 0), (8, 9)}
  • Function #4 {(9, 19), (34, 5), (6, 17), (8, 19)}

If an element in the range repeats, like 6 in function #2 or 19 in function #4, then you do not have a 1 to 1 function.

Relation #1 and Relation #3 are both one-to-one functions.

Problem 3

Is the function below a one to-one function?

one to one function

Yes, because every element in the range is matched with only 1 element in the domain.

Practice Problems - Part II

Use the horizontal line test and your knowledge of 1 to 1 functions to determine whether or not each graph below is 1 to 1.

Problem 1
1 to 1 function

Ask yourself: "Can I draw a horizontal line (anywhere) that will hit the graph two times?"

Since the answer is 'yes', this is not a one-to-one function.

Problem 2
horizontal line test diagram

Ask yourself: "Can I draw a horizontal line (anywhere) that will hit the graph two times?"

Since the answer is 'no', this is a one-to-one function.

Problem 3
One To One Function Problem

Ask yourself: "Can I draw a horizontal line (anywhere) that will hit the graph two times?"

Since the answer is 'no', this is a 1 to 1 function.

Problem 4

Are all lines one to one like the prior problem was? If not, which types of lines are one to one and which types are not?

Vertical lines such as x = 2 are not functions at all.

Horizontal linessuch as y = 9 are functions but they are not 1 to 1 functions.

All other lines are indeed one to one functions.

Problem 5

Are parabolas 1 to 1?

No

As the picture below shows, parabolas are not one to one.

Picture of the horizontal line test
Worksheet On this Page
Further Reading:
Back to Functions Next to Composition of Functions

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!