Quick Overview
- The Mean Value Theorem is typically abbreviated MVT.
- The MVT describes a relationship between average rate of change and instantaneous rate of change.
- Geometrically, the MVT describes a relationship between the slope of a secant line and the slope of the tangent line.
- Rolle's Theorem (from the previous lesson) is a special case of the Mean Value Theorem.
- The MVT has two hypotheses (conditions). Specifically,
- continuity on $$[a,b]$$
- and differentiability on $$(a,b)$$.
-
If the two hypotheses are satisfied, then
$$ f'(c) = \frac{f(b)-f(a)}{b-a} $$
for some $$c\in(a,b)$$.
Basic Idea (Graphical)
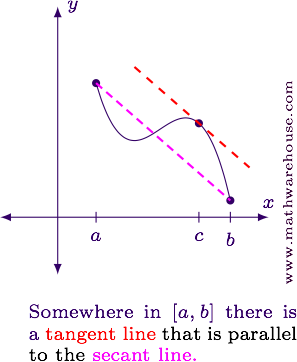
Suppose we are looking at a function on an interval $$[a,b]$$. The line connecting the endpoints (the $${\color{secondaryColor}secant\hspace{2mm}line}$$) will be parallel to at least one of the function's $${\color{importantColor}tangent\hspace{2mm}lines.}$$
In order for this to be true, the function has to be continuous and differentiable on the interval.
Basic Idea (Physical)
Suppose two boats travel the same distance in the same amount of time (perhaps they tie in a race). Also, suppose the first boat drove at a constant speed for the entire trip.
What do we know about the speed of the second boat during the trip?

- Did the second boat have to have a constant speed for the whole trip?
No. It could have driven faster for a while and slower for a while. Or vice versa.
-
Could the second boat have driven faster than the first boat the entire time?
No. If it had, it would have made the trip in less time.
-
Could the second boat have driven slower than the first boat the entire time?
No. If it had, it would have taken longer to make the trip.
Conclusion: The second boat's speed had to be the same as the first boat's at least once during the trip. This is exactly the idea of the Mean Value Theorem.
Formal Statement of the Mean Value Theorem
Suppose $$f(x)$$ is continuous on $$[a,b]$$ and differentiable on $$(a,b)$$. Then there is a point at $$c\in(a,b)$$ where
$$ \frac{f(b)-f(a)}{b-a} = f'(c) $$
Understanding the MVT Equation


Understanding the Hypotheses (the Conditions)
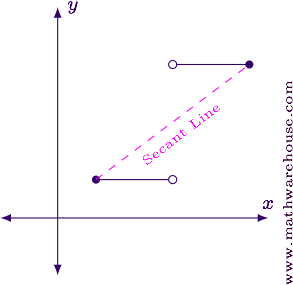
Why is Continuity Necessary?
As shown in the graph below, a discontinuous function could have tangent lines that aren't parallel to the secant line anywhere on the interval (the tangent lines have a slope of $$m=0$$ since the function consists of horizontal line segments).
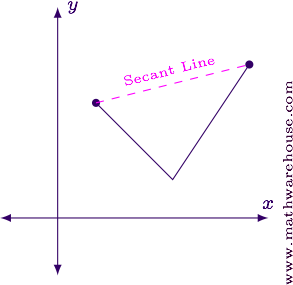
Why is Differentiability Necessary?
The graph below shows what can happen if a continuous function is not differentiable over the interval. Notice that the slope of the tangent lines are not parallel to the slope of the secant line anywhere on the interval (the slopes of the tangent lines are constant, but not equal to the slope of the secant line).
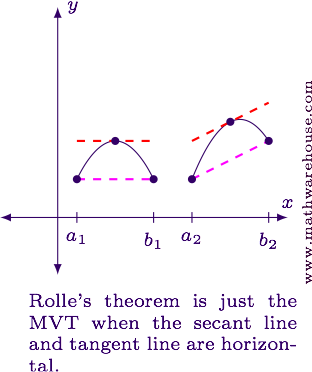
Relationship to Rolle's Theorem
If the two endpoints on the interval happen to have the same function value (so $$f(a) = f(b)$$), then the left-hand side of the MVT equation becomes zero. This is exactly the equation from Rolle's Theorem:
$$0 = f'(c)$$.
Graphically, you can see that Rolle's Theorem is just a special case of the MVT.
Examples of Common Questions
Example 1
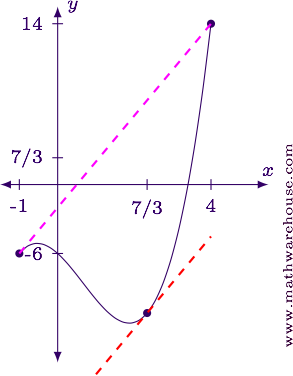
Suppose $$f(x) = x^3 - 2x^2-3x-6$$ over $$[-1, 4]$$. What value of $$x$$ satisfies the the Mean Value Theorem?
Step 1Find the slope of the secant line.
$$ \begin{align*} f(-1) & = (-1)^3 - 2(-1)^2-3(-1)-6 = - 6\\[6pt] f(4) & = (4)^3 - 2(4)^2 -3(4) - 6 = 14\\[6pt] m & = \frac{14 - (-6)}{4-(-1)} = \frac{20} 5 = 4 \end{align*} $$
Step 2Find $$f'(x)$$.
$$ f'(x) = 3x^2 - 4x -3 $$
Step 3Determine where $$f'(x)$$ is equal to the slope found in step 1.
$$ \begin{align*} 3x^2 - 4x -3 & = 4\\ 3x^2 - 4x - 7 & = 0\\ (3x-7)(x+1) & = 1\\ x = \frac 7 3 & \quad x = -1 \end{align*} $$
The MVT guarantees that $$c\in(a,b)$$, and since $$\frac 7 3 \in (-1,4)$$ this is the value we are looking for.
Note, the $$x = -1$$ is excluded since $$-1 \not \in (-1,4)$$.
Answer$$x = \frac 7 3$$ satisfies the MVT.
For reference, below is the graph of the function with one of the tangent lines and the secant line.
Example 2
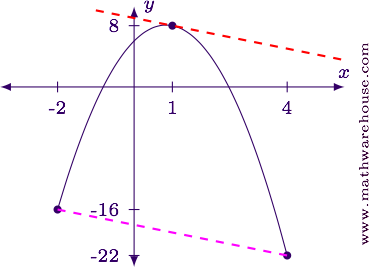
Suppose $$f(x) = 6+5x-3x^2$$ over $$[-2,b]$$. Find the value of $$b$$ so that the Mean Value Theorem is satisfied at $$x = 1$$.
Step 1Find $$f'(1)$$.
$$ \begin{align*} f'(x) & = 5 - 6x\\ f'(1) & = 5-6(1) = -1 \end{align*} $$
Step 2Find the slope of the secant line connecting the endpoints of the interval.
$$ \begin{align*} m & = \frac{f(b)-f(-2)}{b - (-2)}\\[6pt] & = \frac{6 + 5b - 3b^2 - (6 + 5(-2) - 3(-2)^2)}{b - (-2)}\\[6pt] & = \frac{6 + 5b - 3b^2 - (-16)}{b + 2}\\[6pt] & = \frac{22 + 5b - 3b^2}{b + 2} \end{align*} $$
Step 3Determine the value(s) of $$b$$ where the value of the slope found in step 2 is equal to the derivative value found in step 1.
$$ \begin{align*} \frac{22 + 5b - 3b^2}{b + 2} & = -1\\[6pt] 22 + 5b - 3b^2 & = -1(b+2)\\[6pt] 22 + 5b - 3b^2 & = -b-2\\[6pt] 24 + 6b - 3b^2 & = 0\\[6pt] 3b^2 - 6b - 24 & = 0\\[6pt] b^2 - 2b - 8 & = 0\\[6pt] (b-4)(b+2) & = 0\\[6pt] b = 4 & \quad b = -2 \end{align*} $$
We already know the left-hand value of the interval is $$x=-2$$, so the right-hand value is $$x = 4$$.
AnswerWe can use the interval $$\displaystyle \left[-2, 4\right]$$.
For reference, below is the graph of the function, the secant line and the tangent line at $$x=1$$.
How to Prove the Mean Value Theorem
Let's use $$f(x)$$ to represent the function and $$\ell(x)$$ to represent the secant line connecting the endpoints.
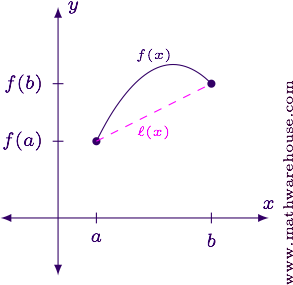
The equation in the MVT says the slope of the tangent line is equal to the slope of the secant line. The slope of the tangent line is $$f'(c)$$ and the slope of the secant line is $$\ell'(c)$$.
(1) (2) $$ \begin{align} {\color{secondaryColor}\frac{f(b) - f(a)}{b-a}} & = f'(c)\\[6pt] {\color{secondaryColor}\ell'(c)} & = f'(c) \end{align} $$
Now, if we subtract one side from the other we get
(3) $$ \begin{equation} f'(c) - {\color{secondaryColor}\ell'(c)} = 0. \end{equation} $$
If we define a new function as $$h(x) = f(x) - \ell(x)$$ then
$$ h'(x) = f'(x) - \ell'(x) $$
and
$$ h'(c) = f'(c) - \ell'(c). $$
So, equation (3) can be written
(4) $$ \begin{equation}h'(c) = 0.\end{equation} $$
This function we've defined, $$h(x) = f(x) - \ell(x)$$, meets all three criteria for Rolle's Theorem:
- Continuity: We know $$f(x)$$ is continuous (by assumption) and $$\ell(x)$$ is continuous since it is just a linear function. Therefore, $$h(x)$$ is continuous since it is the difference between two continuous functions.
- Differentiability: Likewise, both $$f(x)$$ and $$\ell(x)$$ are differentiable, so $$h(x)$$) is too.
- Finally, $$h(a) = f(a) - \ell(a) = 0$$ and $$h(b) = f(b)-\ell(b) = 0$$ so $$h(a) = h(b)$$.
Now we use this line of reasoning in reverse to prove the MVT:
- Start with a function,$$f(x)$$, that is continuous and differentiable over the interval.
- Define two new functions: $$\ell(x)$$ is the equation of the secant line and $$h(x) = f(x) - \ell(x)$$.
- Note that $$h(x)$$ meets the conditions for Rolle's Theorem.
- That means $$h'(c) = 0$$ for some $$c\in[a,b]$$.
- We know $$h'(c) = f'(c) - \ell'(c)$$.
- This means
$$ \begin{align*} f'(c) - \ell'(c) & = 0\\ f'(c) & = \ell'(c)\\ f'(c) & = \frac{f(b)-f(a)}{b-a} \end{align*} $$
And we're done.
Importance of the Mean Value Theorem
Many students see the MVT as a trivial curiosity, but to the mathematician it plays a vital role in establishing the truths in calculus. Here is a quote from two important mathematicians who understood this difference of viewpoints.
In our next lesson we'll examine some consequences of the Mean Value Theorem.


















