Quick Overview
- The first derivative primarily tells us about the direction the function is going. That is, it tells us if the function is increasing or decreasing.
- The first derivative can be interpreted as an instantaneous rate of change.
- The first derivative can also be interpreted as the slope of the tangent line.
The Derivative as the Slope of a Tangent Line
Recall that the definition of the derivative is
$$ \displaystyle\lim_{h\to 0} \frac{f(x+h)-f(x)}{(x+h) - x}. $$
Without the limit, this fraction computes the slope of the line connecting two points on the function (see the left-hand graph below).
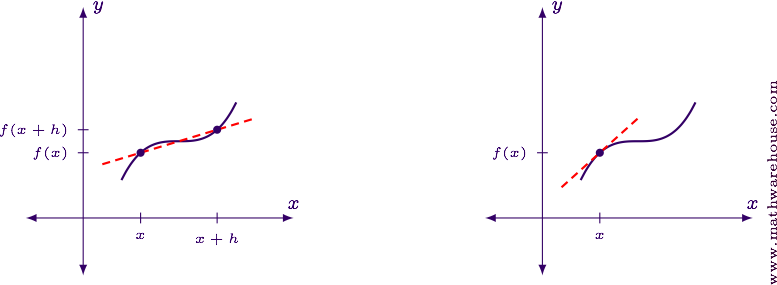
The only thing the limit does is to move the two points closer to each other until they are right on top of each other. But the fundamental calculation is still a slope. So the end result is the slope of the line that is tangent to the curve at the point $$(x, f(x))$$.
Example 1
Suppose $$f(x) = 5x^3 - 8x$$. Determine the slope of the tangent line at $$x = 1$$.
Step 1Find the first derivative.
$$ f'(x) = 15x^2 - 8 $$
Step 2Evaluate $$f'(1)$$.
$$ f'(1) = 15(1)^2 - 8 = 7 $$
AnswerThe tangent line at $$x = 1$$ has a slope of $$m = 7$$.
Increasing and Decreasing
The sign of the derivative at a particular point will tell us if the function is increasing or decreasing near that point. This is readily apparent when we think of the derivative as the slope of the tangent line. As shown in the two graphs below, when the slope of the tangent line is positive, the function will be increasing at that point. Likewise, when the slope of the tangent line is negative, the function will be decreasing.
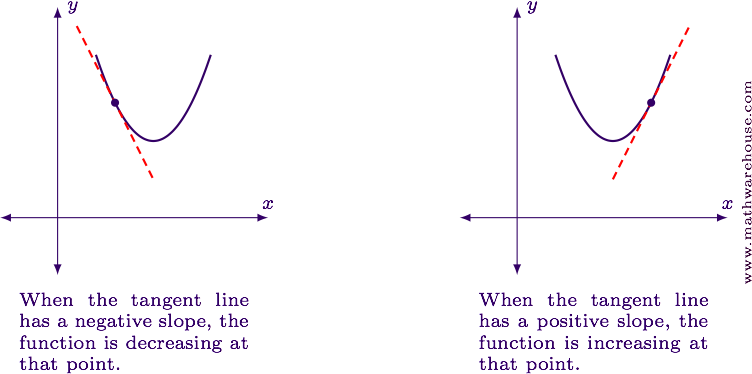
We always read graphs from left to right. So to say a function is increasing, that means that as we look left to right, the function values are getting larger---higher up the $$y$$-axis.
Likewise, a decreasing function's $$y$$-values are getting smaller as we look left to right.
Example 2
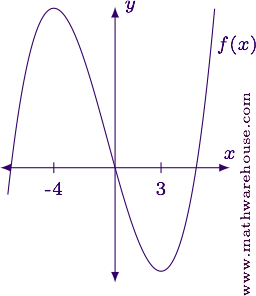
Suppose $$f(x) = 2x^3 + 3x^2 - 72x$$. Determine the intervals over which the function is increasing, and the intervals over which the function is decreasing.
Step 1Find the first derivative.
$$ f'(x) = 6x^2 + 6x - 72 = 6(x^2 + x - 12) = 6(x+4)(x-3) $$
Step 2Sketch a quick graph of the derivative.

Interpret the graph.
We know that when the derivative is positive, the function is increasing. The graph above shows that the derivative is positive (i.e., above the $$x$$-axis) when $$x< -4$$ and when $$x > 3$$.
We can also see that the derivative is negative (below the $$x$$-axis) when $$-4<x<3$$.
AnswerThe function is increasing on the intervals from $$(-\infty,-4)\cup(3,\infty)$$. Likewise, the function is decreasing over the interval $$(-4,3)$$.
The graph of the function is shown below for reference.
The Derivative as a Rate of Change
Suppose $$D(t)$$ represents a runner's distance from the starting line. Then, the derivative of $$D(t)$$ is given by
$$D'(t) = \lim_{h\to 0}\frac{D(t+h) - D(t)}{(t+h)-t}$$
Without the limit, the fraction represents
$$ \begin{align*} \frac{D(t+h) - D(t)}{(t+h)-t} & = \frac{\mbox{Distance run between the two times}}{\mbox{The time elapsed}}\\[6pt] & = \frac{\mbox{Change in Distance}}{\mbox{Change in Time}}\\[6pt] & = \mbox{Average rate of change in distance with respect to time}\\[6pt] & = \mbox{Average Velocity} \end{align*} $$
As we apply the limit, the time elapsed approaches zero. The value of the limit is therefore the velocity at a particular time. This is still a rate of change, but now it is instantaneous.
Example 3
Suppose a runner's distance from the starting line can be described by the function $$D(t) = 10\sqrt{t} + 5$$ for all values of $$t\in(0,16)$$, where $$t$$ is in seconds and distance is in meters. What is the runner's velocity at $$t = 9$$?
Step 1Find the first derivative.
Since $$D(t) = 10t^{1/2} + 5$$ we have
$$ D'(t) = 5t^{-1/2} = \frac 5 {\sqrt t} $$
Step 2Evaluate $$D'(9)$$.
$$ D'(9) = \frac 5 {\sqrt 9} = \frac 5 3 $$
Step 3Interpret the numerical value.
Since the derivative is positive, we know the function is increasing. That means the runner's distance from the start line is increasing, so the runner is moving away from the start line.
The value of the derivative tells us how fast the runner is moving. The sign of the derivative tells us in what direction the runner is moving.
AnswerAfter 9 seconds, the runner is moving away from the start line at a rate of $$\frac 5 3\approx 1.67$$ meters per second.
Example 4
Suppose $$B(t)$$ represents the number of books sold at a bookstore during the $$t^{th}$$ hour of business. What does the equation $$B'(4) = 25$$ mean in terms of sales and time?
Step 1Identify the units of the derivative.
$$ B'(t) = \frac{dB}{dt} = \frac{\mbox{Change in the number of books}}{\mbox{Change in time}} = \frac{\mbox{# of Books}}{\mbox{hours}} $$
The units of the derivative are: books sold per hour.
Answer$$B'(4)=25$$ means that during the 4th hour of business, the books were selling at a rate of 25 books per hour.
Practice Problems
Find the first derivative.
$$ f'(x) = \cos x $$
Evaluate $$f'\left(\frac \pi 3\right)$$.
$$ f'\left(\frac \pi 3\right) = \cos \frac \pi 3 = \frac 1 2 $$
$$m = \frac 1 2$$
Find $$f'(x)$$.
$$ f'(x) = 15e^{3x} $$
Evaluate $$f'(0)$$.
$$ f'(0) = 15e^0 = 15(1) = 15 $$
$$m = 15$$
Find the first derivative.
$$ f'(x) = \frac 1 2 x - 6 $$
Determine where $$f'(x) > 0$$.
$$ \begin{align*} f'(x) & > 0\\[6pt] \frac 1 2 x - 6 & > 0\\[6pt] \frac 1 2 x & > 6\\[6pt] x & > 12 \end{align*} $$
Since the derivative is linear and is positive when $$x>12$$, we know the derivative will be negative when $$x < 12$$.
The function is increasing over $$(12,\infty)$$ and decreasing over $$(-\infty,12)$$.
Find the first derivative of the function. Note that the second term of the function (the $$x(x-2)^3$$ term) will require the product rule.
$$ \begin{align*} f'(x) & = 4(x-2)^3 + (1)(x-2)^3 + 3x(x-2)^2(1)\\[6pt] & = 4(x-2)^3 + (x-2)^3 + 3x(x-2)^2\\[6pt] & = 5(x-2)^3 + 3x(x-2)^2 \end{align*} $$
Simplify the derivative by factoring.
$$ \begin{align*} f'(x) & = 5\blue{(x-2)^3} + 3x\blue{(x-2)^2}\\[6pt] & = \blue{(x-2)^2}\left[5\blue{(x-2)} + 3x\right]\\[6pt] & = (x-2)^2(5x - 10 + 3x)\\[6pt] & = (x-2)^2(8x-10)\\[6pt] & = 2(x-2)^2(4x-5) \end{align*} $$
Examine the graph of $$f'(x)$$.
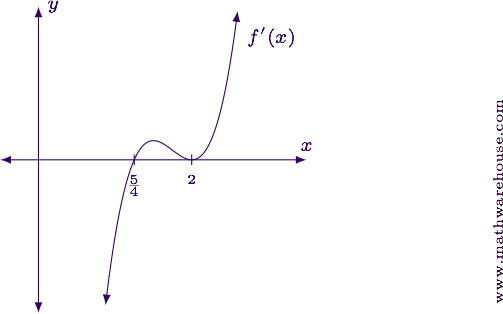
We can see in the graph that the derivative is negative (below the $$x$$-axis) when $$x<\frac 5 4$$. We can also see that the derivative is positive (above the $$x$$-axis) when $$\frac 5 4 < x < 2$$ and $$x > 2$$.
The function is decreasing over the interval $$(-\infty, 5/4)$$. Likewise, the function is increasing over $$(5/4, 2)\cup(2,\infty)$$.
Find the derivative.
$$ A'(t) = 8 - 4t $$
Evaluate $$A'(3)$$.
$$ A'(3) = 8 -4(3) = 8 - 12 = -4 $$
Determine the units of the derivative.
$$ \begin{align*} A'(t) & = \frac{dA}{dt}\\[6pt] & = \frac{\mbox{Change in altitude}}{\mbox{Change in time}}\\[6pt] & = \frac{\mbox{Change in thousands of feet}}{\mbox{Change in hours}}\\[6pt] & \Rightarrow \mbox{thousands of feet per hour} \end{align*} $$
Interpret the sign of the derivative.
Since the derivative is negative, we know the function (altitude) is decreasing. So the plane must be descending.
After 3 hours of flight, the plane is descending at a rate of 4000 feet per hour. This is roughly 0.75 miles per hour of descent.
Find $$P'(x)$$.
$$ P'(x) = -2x + 13 $$
Evaluate $$P'(15)$$.
$$ P'(15) = -2(15) + 13 = 13 - 30 = -17 $$
Determine the units of the derivative.
$$ \begin{align*} P'(x) & = \frac{dP}{dx}\\[6pt] & = \frac{\mbox{Change in profit}}{\mbox{Change in amount sold}}\\[6pt] & = \frac{\mbox{thousands of dollars}}{\mbox{tons of goods}}\\[6pt] & = \mbox{thousand dollars per ton of goods} \end{align*} $$
Interpret the sign of the derivative.
Since the derivative is negative, the function (the profit) is decreasing.
When sales are at 15 tons, profit is decreasing at a rate of 17 thousand dollars per ton. That is, if sales were to increase, profit would be expected to fall at that rate.
Note: In business, selling more doesn't necessarily mean greater profit. If costs are too high, producing more goods to sell can cost more than the money earned from selling the goods.
Determine the units of the derivative.
$$ \begin{align*} B'(t) & = \frac{dB}{dt}\\[6pt] & = \frac{\mbox{Change in blood sugar}}{\mbox{Change in time}}\\[6pt] & = \frac{\mbox{Change in milligrams per deciliter}}{\mbox{Change in minutes}}\\[6pt] & = \mbox{milligrams per deciliter per minute} \end{align*} $$
Interpret the sign of the derivative.
Since the derivative is negative, the function (blood sugar level) is decreasing.
After 30 minutes the blood sugar level is decreasing at a rate of 8 milligrams per deciliter per minute.
Identify the units of the derivative.
$$ \begin{align*} L'(t) & = \frac{dL}{dt}\\[6pt] & = \frac{\mbox{Change in length}}{\mbox{Change in time}}\\[6pt] & = \frac{\mbox{Change in mm}}{\mbox{Change in days}}\\[6pt] & = \mbox{millimeters per day} \end{align*} $$
Interpret the sign of the derivative.
Since the derivative is positive, the function (the length) is increasing.
Six days after being trimmed the fingernail is growing faster than 0.08 millimeters per day.
Determine the value of $$t$$ at the point being measured.
Since $$t$$ measures time in minutes since 8am, the time we are interested in is $$t = 30$$.
Determine the value of the derivative.
Since the person's distance is changing at a rate of 400 feet per minute, the value of the derivative is 400.
Determine the sign of the derivative.
Since the distance from home is decreasing, the derivative must be negative.
$$ \displaystyle D'(30) = -400 $$
Determine the value of $$t$$ at the point in time being measured.
Since we are measuring the voltage six seconds after the circuit was switched on, $$t = 6$$.
Determine the value of the derivative.
Since the voltage is increasing at a rate of 0.04 volts per second, the value of the derivative is 0.04.
Determine the sign of the derivative.
Since the voltage is increasing, the derivative is positive.
$$ V'(6) = 0.04\ $$


















