Quick Overview
- Rolle's Theorem talks about derivatives being equal to zero.
- Rolle's Theorem is a special case of the Mean Value Theorem.
-
Rolle's Theorem has three hypotheses:
- Continuity on a closed interval, $$[a,b]$$
- Differentiability on the open interval $$(a,b)$$
- $$f(a)=f(b)$$
Basic Idea
If a function is continuous and differentiable on an interval, and it has the same $$y$$-value at the endpoints, then the derivative will be equal to zero somewhere in the interval.
Graphically, this means there will be a horizontal tangent line somewhere in the interval, as shown below.
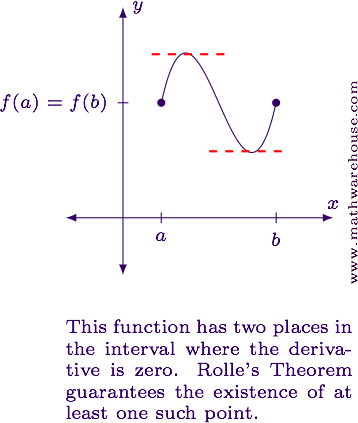
Formal Statement
Suppose $$f(x)$$ is continuous on $$[a,b]$$, differentiable on $$(a,b)$$ and $$f(a) = f(b)$$. Then there exists some point $$c\in[a,b]$$ such that $$f'(c) = 0$$.
Understanding the Theorem
Why Is Continuity Necessary?
Functions that aren't continuous on $$[a,b]$$ might not have a point that has a horizontal tangent line. The graphs below are examples of such functions.
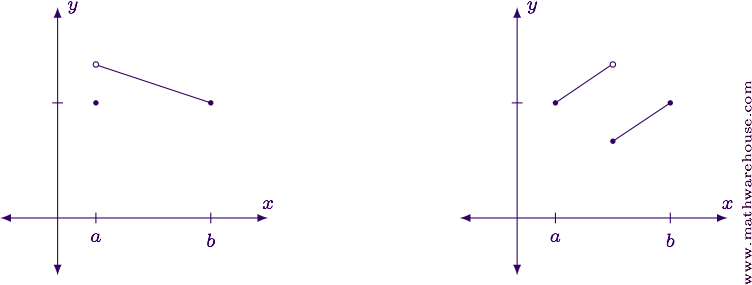
Why is Differentiability Necessary?
Functions that are continuous but not differentiable everywhere on $$(a,b)$$ will either have a corner or a cusp somewhere in the inteval. When this happens, they might not have a horizontal tangent line, as shown in the examples below.
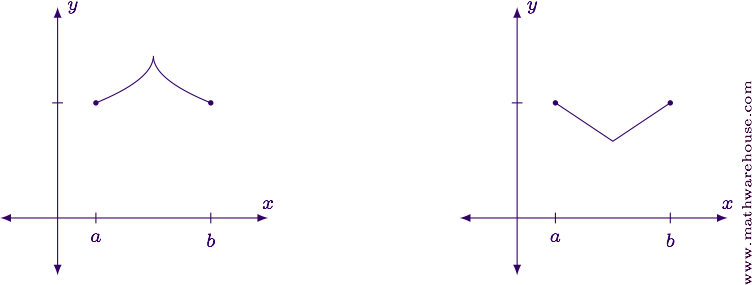
Proving the Theorem
When proving a theorem directly, you start by assuming all of the conditions are satisfied. So, our discussion below relates only to functions
- that are continuous,
- that are differentiable,
- and have $$f(a) = f(b)$$.
With that in mind, notice that when a function satisfies Rolle's Theorem, the place where $$f'(x) = 0$$ occurs at a maximum or a minimum value (i.e., an extrema).
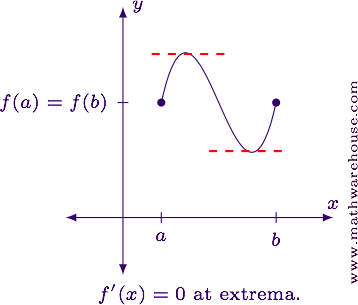
How do we know that a function will even have one of these extrema?
The Extreme Value Theorem! (if you want a quick review, click here). This theorem says that if a function is continuous, then it is guaranteed to have both a maximum and a minimum point in the interval.
Now, there are two basic possibilities for our function.
- Case 1: The function is constant.
- Case 2: The function is not constant.
Case 1: The function is constant
If the function is constant, its graph is a horizontal line segment.
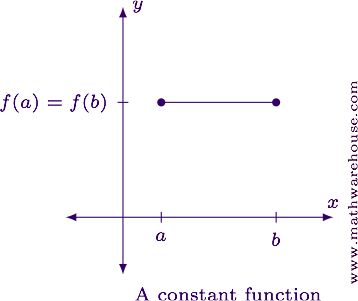
In this case, every point satisfies Rolle's Theorem since the derivative is zero everywhere. (Remember, Rolle's Theorem guarantees at least one point. It doesn't preclude multiple points!)
Case 2: The function is not constant.
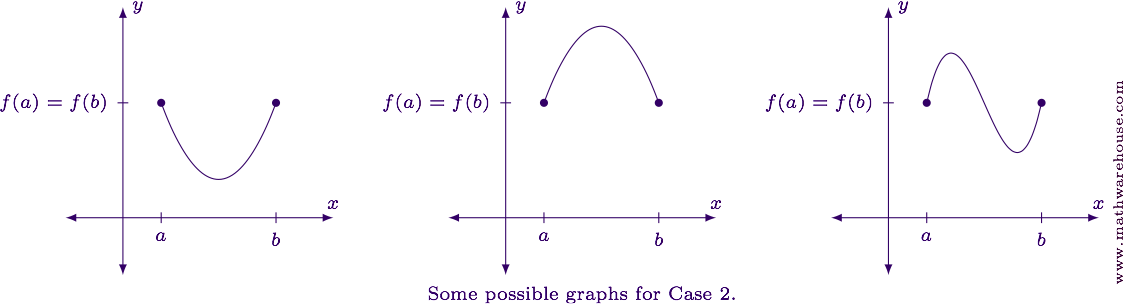
Since the function isn't constant, it must change directions in order to start and end at the same $$y$$-value. This means somewhere inside the interval the function will either have a minimum (left-hand graph), a maximum (middle graph) or both (right-hand graph).
So, now we need to show that at this interior extrema the derivative must equal zero. The rest of the discussion will focus on the cases where the interior extrema is a maximum, but the discussion for a minimum is largely the same.
Possibility 1: Could the maximum occur at a point where $$f'>0$$?
No, because if $$f'>0$$ we know the function is increasing. But it can't increase since we are at its maximum point.
Possibility 2: Could the maximum occur at a point where $$f'<0$$?
No, because if $$f'<0$$ we know that function is decreasing, which means it was larger just a little to the left of where we are now. But we are at the function's maximum value, so it couldn't have been larger.
Since $$f'$$ exists, but isn't larger than zero, and isn't smaller than zero, the only possibility that remains is that $$f' = 0$$.
And that's it! We showed that the function must have an extrema, and that at the extrema the derivative must equal zero!
Historical Background
Michel Rolle was a french mathematician who was alive when Calculus was first invented by Newton and Leibnitz. At first, Rolle was critical of calculus, but later changed his mind and proving this very important theorem.
Rolle's Theorem was first proven in 1691, just seven years after the first paper involving Calculus was published.
Practice Problems
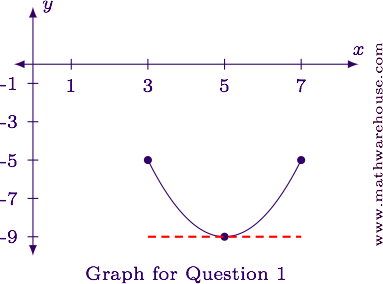
Verify the three hypotheses.
Continuity: The function is a polynomial, and polynomials are continuous over all real numbers.
Differentiability: Again, since the function is a polynomial, it is differentiable everywhere.
Endpoints are Equal:
$$ \begin{align*}% f(3) & = 3^2 - 10(3) + 16 = 9 - 30 + 16 = - 5\\ f(7) & = 7^2 -10(7) + 16 = 49 - 70 + 16 = -5 \end{align*} $$
Find the derivative of the function.
$$ f'(x) = 2x - 10 $$
Set $$f'(x) = 0$$ and solve.
$$ \begin{align*} f'(x) & = 0\\[6pt] 2x - 10 & = 0\\[6pt] 2x & = 10\\[6pt] x & = 5 \end{align*} $$
Find $$f(5)$$.
$$ f(5) = 5^2 - 10(5) + 16 = -9 $$
The point in $$[3,7]$$ where $$f'(x)=0$$ is $$(5,-9)$$.
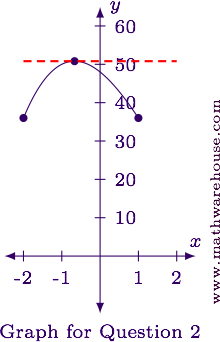
Verify the three hypotheses.
Continuity: The function is a polynomial, so it is continuous over all real numbers.
Differentiability: Polynomial functions are differentiable everywhere.
Endpoints are Equal:
- $$f(-2) = (-2+3)(-2-4)^2 = (1)(36) = 36$$
- $$f(1) = (1+3)(1-4)^2 = (4)(9) = 36$$
Find the first derivative.
$$ \begin{align*} f'(x) & = (x-4)^2 + (x+3)\cdot 2(x-4)\\[6pt] & = (x-4)\left[(x-4) + 2(x+3)\right]\\[6pt] & = (x-4)\left[x-4+2x+6\right]\\[6pt] & = (x-4)(3x+2) \end{align*} $$
Solve $$f'(x) = 0$$.
$$ \begin{align*} f'(x) & = 0\\[6pt] (x-4)(3x+2) & = 0\\[6pt] x = 4 & \qquad x = -\frac 2 3 \end{align*} $$
Since we are working on the interval $$[-2,1]$$, the point we are looking for is at $$x = -\frac 2 3$$.
Evaluate $$f(-2/3)$$.
$$ \begin{align*} f\left(-\frac 2 3\right) & = \left(-\frac 2 3 + 3\right)\left(-\frac 2 3 - 4\right)^2\\[6pt] & = \left(\frac 7 3\right)\left(- \frac{14} 3\right)^2\\[6pt] & = \left(\frac 7 3\right)\left(\frac{196} 9\right)\\[6pt] & = \frac{1372}{27}\\[6pt] & \approx 50.8148 \end{align*} $$
The point in $$[-2,1]$$ where $$f'(x) = 0$$ is at $$\left(-\frac 2 3, \frac{1372}{27}\right)$$.
In order for Rolle's Theorem to apply, all three criteria have to be met. To find out why it doesn't apply, we determine which of the criteria fail.
Check to see if the endpoints are equal.
$$ \begin{align*}% f(1) & = 1 + 1 = 2\\[6pt] f(4) & = 2 + 4(4) - 4^2 = 2+ 16 - 16 = 2 \end{align*} $$
Check to see if the function is continuous over $$[1,4]$$.
The function is piecewise-defined, and each piece itself is continuous. So, we only need to check at the transition point between the two pieces.
Recall that to check continuity, we need to determine if
$$ \displaystyle\lim_{x\to 3^+}f(x) = f(3). $$
Checking $$f(3)$$ we have
$$ f(3) = 3 + 1 = 4. $$
Next, checking the limit, we have
$$ \begin{align*}% \lim_{x\to 3^+} f(x) & = \lim_{x\to 3^+} \left(2 + 4x - x^2\right)\\[6pt] & = 2 + 4(3) - 3^2\\[6pt] & = 5 \end{align*} $$
Since $$f(3) \neq \lim\limits_{x\to3^+} f(x)$$ the function is not continuous at $$x = 3$$.
Rolle's Theorem doesn't apply in this situation since the function isn't continuous at all points on $$[1,4]$$.

In order for Rolle's Theorem to apply, all three criteria have to be met. To find out why it doesn't apply, we determine which of the criteria fail.
Check to see if the endpoints are equal.
$$ \begin{align*} f(2) & = \frac 1 2(2 - 6)^2 - 3 = \frac 1 2(-4)^2 - 3 = 8 - 3 = 5\\ f(10) & = 10 - 5 = 5 \end{align*} $$
Check for continuity over $$[2,10]$$.
The function is piecewise defined, and both pieces are continuous. So the only point we need to be concerned about is the transition point between the two pieces.
The transition point is at $$x = 4$$, so we need to determine if
$$ \displaystyle\lim_{x\to4} f(x) = f(4). $$
Function Value
$$ f(4) = \frac 1 2(4-6)^2-3 = 2-3 = -1 $$
Limit from the Left
$$ \begin{align*}% \displaystyle\lim_{x\to4^-} f(x) & = \displaystyle\lim_{x\to4^-}\left[\frac 1 2(x-6)^2-3\right]\\[6pt] & = \frac 1 2(4-6)^2-3\\[6pt] & = 2 - 3\\ & = -1 \end{align*} $$
Limit from the Right
$$ \begin{align*}% \displaystyle\lim_{x\to4^+} f(x) & = \displaystyle\lim_{x\to4^+}\left(x-5\right)\\[6pt] & = 4-5\\[6pt] & = -1 \end{align*} $$
The two one-sided limits are equal, so we conclude $$\displaystyle\lim_{x\to4} f(x) = -1$$.
Since $$f(4) = \displaystyle\lim_{x\to4}f(x) = -1$$, we conclude the function is continuous at $$x=4$$ and therefore the function is continuous on $$[2,10]$$.
Differentiability.
Since each piece itself is differentiable, we only need to determine if the function is differentiable at the transition point at $$x = 4$$.
From the left, the derivative would be
$$ f'(x) = x-6\longrightarrow f'(4) = 4-6 = -2. $$
And from the right, the derivative is
$$ f'(x) = 1 $$
The slope of the tangent line is different when we approach $$x = 4$$ from the left of from the right. This means at $$x = 4$$ the function has a corner (see the graph below).

Consequently, the function is not differentiable at all points in $$(2,10)$$.
Rolle's Theorem does not apply to this situation because the function is not differentiable on the interval.


















