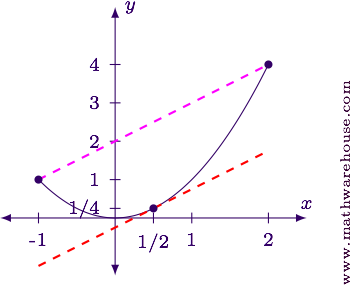
Find the coordinates of the endpoints of the function.
$$ \begin{align*} f(-1) & = (-1)^2 = 1\\ f(2) & = 2^2 = 4 \end{align*} $$
The coordinate points are $$(-1,1)$$ and $$(2,4)$$.
Find the slope of the secant line.
$$ m = \frac{4-1}{2-(-1)} = \frac 3 {2+1} = 1 $$
Find $$f'(x)$$.
$$ f'(x) = 2x $$
Determine where the derivative equals the slope of the secant line.
$$ \begin{align*} f'(x) & = 1\\ 2x & = 1\\ x & = \frac 1 2 \end{align*} $$
Find the $$y$$-coordinate of the point on the function at $$x=\frac 1 2$$.
$$ f\left(\frac 1 2\right) = \left(\frac 1 2\right)^2 = \frac 1 4 $$
The point on $$f(x)$$ where $$f'$$ equals the slope of the tangent line is at $$\left(\frac 1 2, \frac 1 4\right)$$.
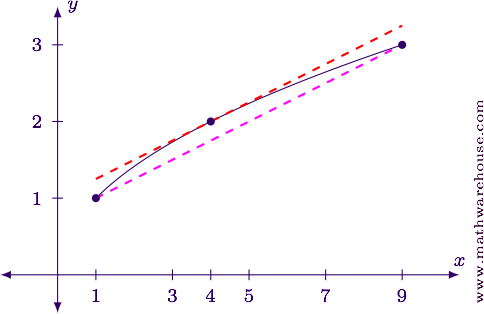
Find the coordinates of the endpoints of the function on the interval.
$$ \begin{align*} f(1) & = \sqrt 1 = 1\\ f(9) & = \sqrt 9 = 3 \end{align*} $$
The endpoints of the function are $$(1,1)$$ and $$(9,3)$$.
Find the slope of the secant line through the endpoints.
$$ \begin{align*} m & = \frac{3-1}{9-1}\\[6pt] & = \frac 2 8\\[6pt] & = \frac1 4 \end{align*} $$
Find the derivative of the function. We first rewrite the function as $$f(x) = x^{1/2}$$.
$$ \begin{align*} f'(x) & = \frac 1 2 x^{-1/2} = \frac 1 {2\sqrt x} \end{align*} $$
Determine where the slopes of the secant and tangent lines are equal.
$$ \begin{align*} \frac 1 {2\sqrt x} & = \frac 1 4\\[6pt] 2\sqrt x & = 4\\[6pt] \sqrt x & = 2\\[6pt] x & = 4 \end{align*} $$
Find the point of tangency at $$x=4$$.
$$ f(4) = \sqrt 4 = 2 $$
The point of tangency is $$(4,2)$$.
The point of tangency is $$(4,2)$$.
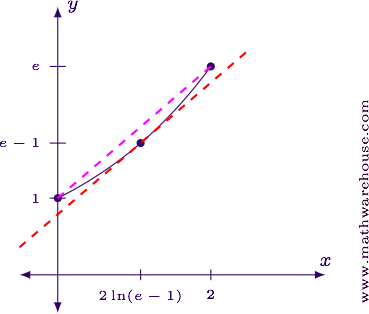
Find the coordinates of the endpoint of the interval.
$$ \begin{align*} f(0) & = e^{0.5(0)} = 1\\[6pt] f(2) & = e^{0.5(2)} = e^1 \approx 2.718 \end{align*} $$
Find the slope of the line connecting the endpoints.
$$ m = \frac{f(2)-f(0)}{2-0} = \frac{e - 1} 2 $$
Find $$f'(x)$$.
$$ f'(x) = 0.5e^{0.5x} $$
Determine where $$f'(x)$$ is equal to the slope we found in step 2.
$$ \begin{align*} 0.5e^{0.5x} & = \frac{e - 1} 2\\[6pt] e^{0.5x} & = e - 1\\[6pt] 0.5x & = \ln(e-1)\\[6pt] x & = 2\ln(e-1) \approx 1.0826 \end{align*} $$
Find the $$y$$-value at the point of tangency.
$$ f\left(2\ln(e-1)\right) = e^{0.5\left(2\ln(e-1)\right)} = e^{\ln(e-1)} = e -1\approx 1.7183 $$
The point of tangency is $$(2\ln(e-1), e-1) \approx (1.0826, 1.7183)$$
Find the value of derivative at $$x = 2$$.
$$ \begin{align*} f'(x) & = 4(x-1)\\ f'(2) & = 4(2-1) = 4 \end{align*} $$
Find the formula for the slope of the secant line over $$[a,3]$$.
$$ \begin{align*} m & = \frac{f(3)-f(a)}{3-a}\\[6pt] & = \frac{2(3-1)^2-3 - \left[2(a-1)^2-3\right]}{3-a}\\[6pt] & = \frac{8 - 2(a-1)^2}{3-a} \end{align*} $$
Equate the formula in step 2 to the derivative value from step 1 and solve for $$a$$.
$$ \begin{align*} \frac{8 - 2(a-1)^2}{3-a} & = 4\\[6pt] 8 - 2(a-1)^2 & = 4(3-a)\\[6pt] 8 - 2(a^2-2a+1) & = 12-4a\\[6pt] 8 -2a^2+4a-2 & = 12-4a\\[6pt] -2a^2+8a -6 & =0\\[6pt] a^2 - 4a + 3 & = 0\\[6pt] (a-1)(a-3) & = 0\\[6pt] a = 1 & \qquad a = 3 \end{align*} $$
We know the right-hand value of the interval is at $$x = 3$$, so the right-hand value will be $$a = 1$$.
The interval is $$[1, 3]$$.
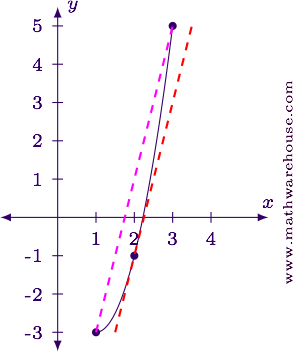
Find the value of $$f'(3)$$.
$$ \begin{align*} f(x) & = 2\sqrt{x+1} = 2(x+1)^{1/2}\\ f'(x) & = 2\cdot \frac 1 2(x+1)^{-1/2} = \frac 1 {\sqrt{x+1}}\\ f'(3) & = \frac 1 {\sqrt 4} = \frac 1 2 \end{align*} $$
Find the slope of the secant line over the interval $$[-1,b]$$.
$$ \begin{align*} m & = \frac{2\sqrt{b+1} - 2\sqrt{-1+1}}{b-(-1)} = \frac{2\sqrt{b+1}}{b+1} \end{align*} $$
Equate the slope from step 2 to the derivative value from step 1. Solve for $$b$$.
$$ \begin{align*} \frac{2\sqrt{b+1}}{b+1} & = \frac 1 2\\[6pt] 4\sqrt{b+1} & = b+1\\[6pt] 16(b+1) & = (b+1)^2\\[6pt] 16b+16 & = b^2+2b+1\\[6pt] b^2 -14b-15 & = 0\\[6pt] (b-15)(b+1) & = 0\\[6pt] b = 15 & \qquad b = -1 \end{align*} $$
Since the left-hand side of the interval is at $$x=-1$$, we conclude the right-hand side is $$b = 15$$.
The interval is $$[1,15]$$.
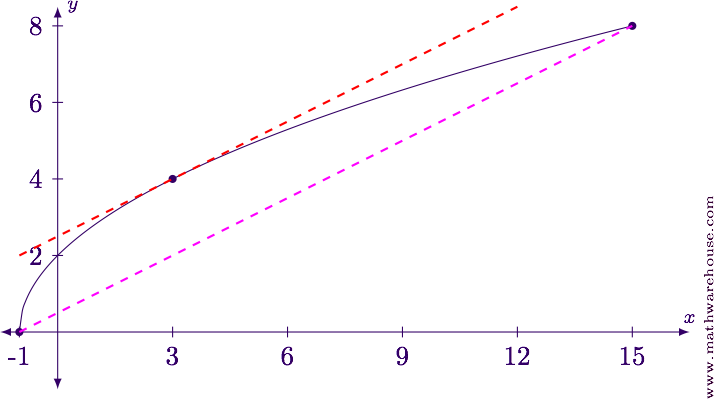
Is the function continuous on $$[-1,3]$$?
Since the function is piece-wise defined and each piece is itself continuous, we only need to determine if the function is continuous at the transitions point at $$x=2$$.
To confirm this, we will check to see if
$$ \displaystyle\lim_{x\to2^-}f(x) = \displaystyle\lim_{x\to2^+}f(x) = f(2). $$
Limit from the left: $$\displaystyle \lim_{x\to2^-}f(x) = \lim_{x\to2^-}(x^2-3x) = 2^2-3(2)=-2$$
Limit from the right: $$\displaystyle \lim_{x\to2^+}f(x)=\lim_{x\to2^+}(x^3-11x+12) = 2^3-11(2)+12 = -2$$
Function value: $$\displaystyle f(2) = 2^2-3(2) = -2$$
We conclude the function is continuous on the entire interval $$[-1,3]$$.
Checking differentiability.
The derivative of the function is at least
$$ f'(x) = \left\{ \begin{array}{ll} 2x-3,& x < 2\\ 3x^2 -11, & x>2 \end{array} \right. $$
But does the derivative exist at $$x=2$$? To answer this, we need to take the limit of the derivative from the left and from the right. If the two limit values are equal, then the derivative at $$x=2$$ can be defined as this common limit value.
Limit from the left: $$\displaystyle \lim_{x\to2^-}f'(x) = \lim_{x\to2^-}(2x-3) = 2(2)-3=1$$
Limit from the right: $$\displaystyle \lim_{x\to2^+}f'(x) = \lim_{x\to2^+}(3x^2-11) = 3(2^2)-11=1$$
Since the one-sided limits of the derivative are equal, we can define $$f'(2) =1$$, and the function is now differentiable on the interval $$(-1,3)$$.
Since the function is both continuous and differentiable on the interval, the Mean Value Theorem can be applied.
For reference, the function, the secant line and the parallel tangent line is shown below.
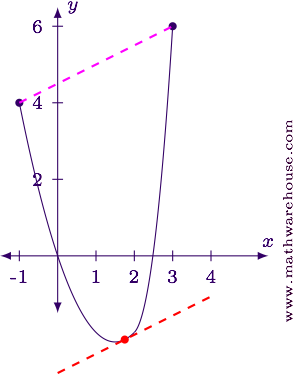
Is the function continuous on the interval $$[0,6]$$?
Since the function is piece-wise defined, and each piece is continuous, we only need to check for continuity at the transition point at $$x=4$$.
To do that, we need to determine if
$$ \displaystyle\lim_{x\to4^-}f(x) = \displaystyle\lim_{x\to4^+}f(x) = f(4). $$
Limit from the left: $$\displaystyle \lim_{x\to4^-} f(x) = \lim_{x\to4^-}\sqrt{x^2+9} = \sqrt{4^2+9} = \sqrt{25} = 5$$
Limit from the right: $$\displaystyle \lim_{x\to4^+} f(x) = \lim_{x\to4^+} 6-(x-5)^2 = 6 - (6-5)^2 = 6-1=5$$
Function value: $$\displaystyle f(4) = \sqrt{4^2+9} = \sqrt{25} = 5$$
We conclude that the function is continuous on $$[0,6]$$.
Is the function differentiable on $$[0,6]$$?
Again, each piece itself is differentiable. We need to see if differentiability holds at the transition point.
The derivative of $$f$$ is, at the very least
$$ f(x) = \left\{ \begin{array}{ll} \frac x {\sqrt{x^2+9}}, & x<4\\ -2(x-5), & x > 4 \end{array} \right. $$
To find out if the function is also differentiable at $$x=4$$, we check the left and right-hand limits of $$f'$$ as $$x\to 4$$. If the values are equal, we can define $$f'(4)$$ to be that value.
Limit from the left: $$\displaystyle \lim_{x\to4^-}f'(x) = \lim_{x\to4^-} \frac x {\sqrt{x^2+9}} = \frac 4 {\sqrt{4^2+9}} = \frac 4 {\sqrt{25}} = \frac 4 5$$
Limit from the right: $$\displaystyle \lim_{x\to4^+}f'(x) = \lim_{x\to4^+} -2(x-5) = -2(4-5) = 2$$
Since the left-hand and right-hand limits are different, we have to conclude that the function is not differentiable at $$x = 4$$, so it is not differentiable on the entire interval.
The Mean Value Theorem cannot be applied to this function on any interval that includes $$x=4$$ as an interior point.
NOTE: The MVT cannot be applied to this function on the interval $$[0,6]$$, but that doesn't mean there isn't a tangent line that is parallel to the secant line. It just means that the MVT cannot guarantee one exists. In fact, for this function, there are two such tangent lines as shown in the graph below.
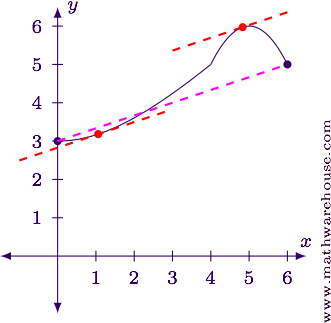
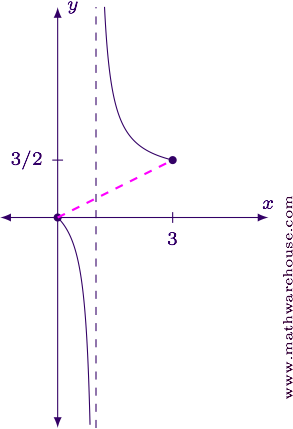
Find the function's endpoints on the interval.
$$ \begin{align*} f(0) & = \frac 0 {0-1} = 0\\[6pt] f(3) & = \frac 3 {3-1} = \frac 3 2 \end{align*} $$
The two coordinate points are $$(0,0)$$ and $$\left(3, \frac 3 2\right)$$
.Find the slope of the secant line connecting the two points you found.
$$ \begin{align*} m & = \frac{\frac 3 2 - 0}{3 - 0}\\[6pt] & = \frac 3 2 \cdot \frac 1 3\\[6pt] & = \frac 1 2 \end{align*} $$
The slope of the secant line is $$m = \frac 1 2$$.
Find the derivative of the function. This will require the quotient rule.
$$ \begin{align*} f'(x) & = \frac{(x-1)\cdot 1 - x(1)}{(x-1)^2}\\[6pt] & = \frac{x-1-x}{(x-1)^2}\\[6pt] & = -\frac 1 {(x-1)^2} \end{align*} $$
Determine where the derivative is equal to $$\frac 1 2$$.
$$ \begin{align*} -\frac 1 {(x-1)^2} & = \frac 1 2\\[6pt] (x-1)^2 & = -2\\[6pt] x-1 & = \sqrt{-2} \end{align*} $$
Since the right-hand side results in the square-root of a negative number, we conclude that there is no $$x$$-value where the derivative is equal to $$\frac 1 2$$.
There is no such point. Explanation of what went wrong:
The Mean Value Theorem only applies to functions that are continuous and differentiable on the interval. However, this function is not continuous at $$x=1$$, so the MVT makes no guarantee. For this particular function, there is no tangent line that is parallel to the secant line on this interval because of the discontinuity.