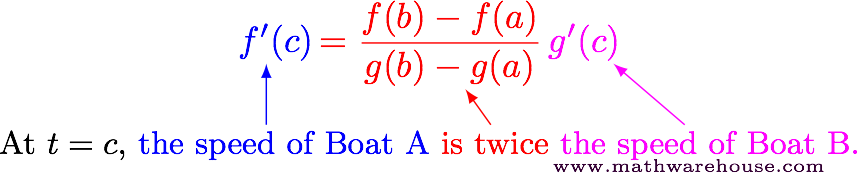Quick Overview
- The mathematician Baron Augustin-Louis Cauchy developed an extension of the Mean Value Theorem.
- This extension discusses the relationship between the derivatives of two different functions.
- Specifically, if $$ \Delta f = k\Delta g $$ then $$ f' = kg' $$ somewhere.
Basic Idea (Physical)
In the lesson on the Mean Value Theorem we thought about a race between two boats. The boats covered the same distance in the same amount of time, and so we concluded they must have been going the same speed sometime during the race.
Let's take that same situation and adjust it slightly. Let's say the two boats are traveling for exactly 15 minutes. At the end of that time, the Boat A covered exactly twice the distance as the Boat B.

What conclusion can we draw about the speeds of the boats?
- Could the speed of Boat A have been more than twice the speed of the second boat for the entire 15 minutes?
No. If that were true, Boat A would have gone more than twice the distance of Boat B. - Could the speed of Boat A have been less than twice the speed of Boat B for the entire 15 minutes?
No. If that were true, Boat A would have traveled less than twice the distance of Boat B.
So in order to travel exactly twice the distance, Boat A’s speed had to be exactly twice the speed of Boat B at least once during the 15 minutes.
Basic Idea (Geometric)
Suppose we have two functions defined on $$ [a,b] $$, and
$$ \begin{align*} f(b) - f(a) & = 6\qquad \mbox{and}\qquad g(b) - g(a) = 3. \end{align*} $$
So the change in $$ f $$ is twice as big as the change in $$ g $$. Then somewhere between $$ a $$ and $$ b $$ is an $$ x $$-value where $$ f' = 2g' $$, as shown in the image below.
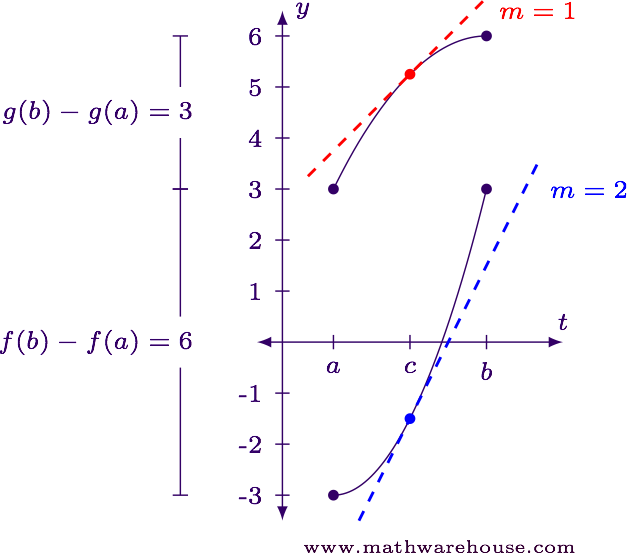
If we think of the curves as hills, then the slope of the tangent lines represents the steepness of the hills. So at $$ x = c $$, the $$ f(x) $$ "hill" is twice a steep as the $$ g(x) $$ "hill".
Examples
Example 1
Suppose $$ f(x) = \frac 1 6x^3 + 2 $$ and $$ g(x) = \frac 1 3(x+2)^2 - 2 $$ over the interval $$ x\in [\xMin, \xMax] $$.
- Determine the value of $$ k $$ so that $$ \Delta f = k\Delta g $$ over $$ [\xMin,\xMax] $$.
- Find a value of $$ c\in (\xMin,\xMax) $$ where $$ f'(c) = k\,g'(c) $$.
Find the values of $$ \Delta f $$ and $$ \Delta g $$ over $$ [\xMin,\xMax] $$.
$$ \begin{align*} \Delta f & = \blue{f(\xMax)} - \red{f(\xMin)} = \left(\blue{\frac 1 6(\xMax)^3 + 2}\right) - \left(\red{\frac 1 6(\xMin)^3 + 2}\right) = \blue{-\frac 5 6} - \red{\left(-\frac{25}{16}\right)} = \frac{35}{48}\\[6pt] \Delta g & = \blue{g(\xMax)} - \red{g(\xMin)} = \left(\blue{\frac 1 3(\xMax+2)^2 - 2}\right) - \left(\red{\frac 1 3(\xMin + 2)^2 - 2}\right) = \blue{0} - \left(\red{- \frac{35}{12}}\right) = \frac{35}{12} \end{align*} $$
Part (a) Step 2Calculate $$k$$.
$$ \begin{align*} \blue{\Delta f} & = k\red{\Delta g}\\[6pt] \blue{\frac{35}{48}} & = k\left(\red{\frac{35}{12}}\right)\\[6pt] k & = \blue{\frac{35}{48}} \cdot \left(\red{\frac{12}{35}}\right) = \frac1 4 \end{align*} $$
Part (b) Step 1Find $$ f' $$ and $$ g' $$.
$$ \begin{align*} f'(x) & = \frac 1 2x^2\\[6pt] g'(x) & = \frac 2 3 (x + 2) \end{align*} $$
Part (b) Step 2Find the value of $$ x\in(\xMin,\xMax) $$ where $$ f'(x) = k\,g'(x) $$ for $$ k= \frac 1 4 $$ as found in part (a).
$$ \begin{align*} f'(x) & = k\cdot g'(x)\\[6pt] \frac 1 2 x^2 & = \frac 1 4\cdot \frac 2 3(x+2)\\[6pt] \frac 1 2 x^2 & = \frac 1 6(x+2)\\[6pt] 3x^2 & = x + 2\\[6pt] 3x^2 - x - 2 & = 0\\[6pt] (3x + 2)(x - 1) & = 0\\[6pt] x = 1 & \text{ and } x = -\frac 2 3 \end{align*} $$
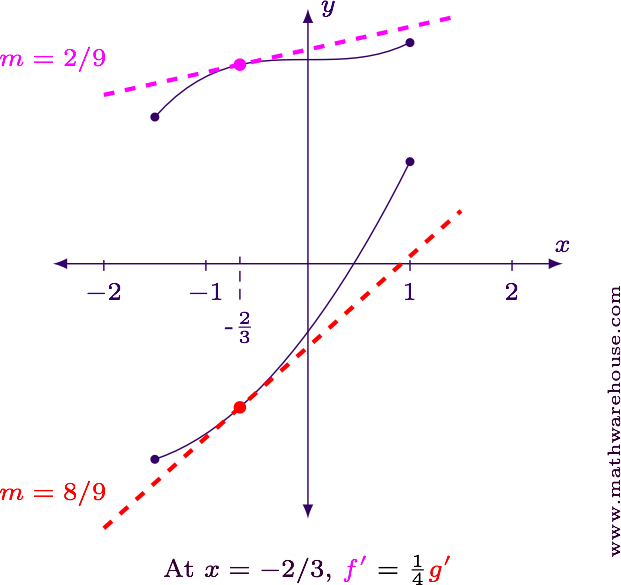
Note that $$ x = -\frac 2 3 $$ is in $$ (\xMin,\xMax) $$, but $$ x = 1 $$ is not. Let's check our answer.
CheckingAt $$ x = -\frac 2 3 $$, we have
$$ \begin{align*} f'\left(-\frac 2 3\right) & = \frac 1 2\left(-\frac 2 3\right)^2 = \frac 2 9\\[6pt] g'\left(-\frac 2 3\right) & = \frac 2 3 \left(-\frac 2 3 + 2\right) = \frac 8 9 \end{align*} $$
and with $$ k = \frac 1 4 $$ we have $$ f'\left(-\frac 2 3\right) = \frac 2 9 = \frac 1 4\cdot \frac 8 9 = k\cdot g'\left(-\frac 2 3\right) $$.
Answer(a) $$ k = \frac 1 4 $$; (b) $$ x = -\frac 2 3 $$
For reference, here is the graph of $$ f(x) $$ and $$ g(x) $$ together with their tangent lines and slopes at the two values found.
The Formalities---Two Versions of Cauchy's Extension
There are two versions of Cauchy's extension of the MVT. One is a little easier to interpret, but is a weaker statement. We'll start with this one, though, because once we understand the weaker version we can just make a small adjustment and we'll be able to understand the more robust version.
Formal Statement of Version 1
Suppose $$ f $$ and $$ g $$ are both continuous on $$ [a,b] $$ and differentiable on $$ (a,b) $$ and $$ f(a)\neq f(b) $$ and $$ g(a)\neq g(b) $$. Then there exists some $$ c\in(a,b) $$ at which
$$ f'(c) = \frac{f(b)-f(a)}{g(b)-g(a)} \cdot g'(c) $$
Understanding the Formal Statement
-
Explanation of the Equation
Let's interpret the equation in terms of the boat race analogy, and let's start with the ugly fraction in the equation.
$$\frac{f(b) - f(a)}{g(b)-g(a)} = \frac{\mbox{Total Distance Traveled by Boat 1}}{\mbox{Total Distance Traveled by Boat 2}}$$
In our discussion about the racing boats, the fraction would be equal to 2 since Boat A traveled twice as far as Boat B.
Since $$ f'(c) $$ and $$ g'(c) $$ would be the speeds of the boats at $$ t = c $$, it is easy to read the equation as
![Cauchy's Mean Value Theorem - Equation Explanation]()
-
Understanding the Hypotheses (the Conditions)
-
Continuity and Differentiability
By now, you probably recognize theses conditions from our discussions of Rolle's Theorem and the Mean Value Theorem. Similar problems occur if we omit these requirements.
-
Endpoints Not Equal
In this first version of Cauchy's extension of the MVT we don't allow $$ g(a)=g(b) $$ or $$ f(a)=f(b) $$ to avoid problems with division by zero. In the more robust, second version the need for this restriction is removed.
-
Proof of Version 1:
$$ h(\blue t) = \frac{f(\blue t) - f(a)}{f(b) - f(a)} - \frac{g(\blue t)-g(a)}{g(b)-g(a)}. $$
Lot's of letters running around up there, so I put the variable $$\blue t$$ in blue. Everything else is a constant.
Let's take a moment to understand this helper function. In the context of the boat example, the entire distance traveled by Boat A is $$ f(b)-f(a) $$. Similarly, if $$ \blue t\in(a,b) $$ then $$ f(\blue t)-f(a) $$ is the distance traveled by Boat A up until time $$ \blue t $$. Then, the ratio
$$ \frac{f(\blue t)-f(a)}{f(b)-f(a)} = \frac{\mbox{distance so far}}{\mbox{total distance}} = \mbox{fraction of total distance traveled by Boat A by time } \blue t. $$
Similarly,
$$ \frac{g(\blue t)-g(a)}{g(b)-g(a)} = \mbox{fraction of total distance traveled by Boat B by time } \blue t. $$
The function $$ h(\blue t) $$ is just the difference between these two ratios. Now, we show that $$ h(\blue t) $$ satisfies the hypotheses of Rolle's theorem.
- Continuity: Since $$ f $$ and $$ g $$ are continuous, and we have specified $$ f(a)\neq f(b) $$ and $$ g(a)\neq g(b) $$ (which avoids division by zero), $$ h(\blue t) $$ will also be continuous.
- Differentiability: Likewise, since $$ f $$ and $$ g $$ are differentiable, so is $$ h(\blue t) $$.
-
Endpoints: $$ h $$ has the same value at the endpoints, as shown below.
$$ \begin{align*} h(\blue a) & = \frac{\overbrace{f(\blue a) - f(a)}^{\mbox{ Numerator = 0}}}{f(b) - f(a)} - \frac{\overbrace{g(\blue a)-g(a)}^{\mbox{ Numerator = 0}}}{g(b)-g(a)}= \frac 0 {f(b)-f(a)} - \frac 0 {g(b)-g(a)} = 0\\[6pt] h(\red b) & = \underbrace{\frac{f(\red b) - f(a)}{f(b) - f(a)}}_{\mbox{ Fraction = 1}} - \underbrace{\frac{g(\red b)-g(a)}{g(b)-g(a)}}_{\mbox{ Fraction = 1}} = 1 - 1 = 0 \end{align*} $$
According to Rolle's theorem there is a $$ c\in(a,b) $$ where $$ h'(c) = 0 $$. Now, $$ h'(\blue t) $$ is
$$ h'(\blue t) = \frac{f'(\blue t)}{f(b)-f(a)} - \frac{g'(\blue t)}{g(b)-g(a)} $$
and plugging in our $$ \blue{t = c} $$ value we get
$$ \begin{align*} h'(\blue c) = \frac{f'(\blue c)}{f(b)-f(a)} - \frac{g'(\blue c)}{g(b)-g(a)} & = 0 \end{align*} $$
With a little adjustment we get
$$ \begin{align*} \frac{f'(\blue c)}{f(b)-f(a)} - \frac{g'(\blue c)}{g(b)-g(a)} & = 0\\[6pt] \frac{f'(\blue c)}{f(b)-f(a)} & = \frac{g'(\blue c)}{g(b)-g(a)} && \mbox{ Add to the other side}\\[6pt] \frac{f'(\blue c)}{f(b)-f(a)} & = \frac 1 {g(b)-g(a)}\cdot g'(\blue c) && \mbox{ Pull \(g'\) off to the side.}\\[6pt] f'(\blue c) & = \frac{f(b)-f(a)}{g(b)-g(a)}\cdot g'(\blue c) && \mbox{ Multiply.} \end{align*} $$
which is what we wanted to show.
Now we turn our attention to the second and stronger version of the theorem.
Why Bother With a
Second Version?
In the first version, one of the conditions was the endpoints of the two functions could not be equal. That is, $$ f(a) \neq f(b) $$ and $$ g(a) \neq g(b) $$, otherwise we would end up with division by zero.
The stronger (better) version of Cauchy's Extension of the MVT eliminates this condition. To do so, we have to adjust the equation in the theorem just a bit, but the meaning of the theorem is still the same.
Formal Statement of Version 2
Suppose $$ f $$ and $$ g $$ are both continuous on $$ [a,b] $$ and differentiable on $$ (a,b) $$. Then there exists a $$ c\in (a,b) $$ where
$$ \Big(g(b)-g(a)\Big)\cdot f'(c) = \Big(f(b)-f(a)\Big)\cdot g'(c). $$
Understanding The Equation in This Version
If you compare this equation to the one from Version 1, you can easily see that we've just multiplied through by the denominator. But now, even if the endpoints are equal, we avoid division by zero (yes, we get multiplication by zero, but that doesn't cause mathematical problems).
Proof of Version 2
When we proved Version 1, we used the helper function
$$ \blue{h(t) = \frac{f(t) - f(a)}{f(b)-f(a)} - \frac{g(t)-g(a)}{g(b)-g(a)}} $$
To prove this version of the function, we have to adjust this helper function by scaling it by its common denominator which is
$$ \red{\Big(f(b)-f(a)\Big)\Big(g(b)-g(a)\Big)}. $$
Let's call our new helper function $$ H(t) $$ and define it as
$$ \begin{align*} H(t) & = \red{\Big(Common \hspace{2mm} Denominator \hspace{2mm} (or \hspace{2mm} CD)\Big)}\cdot \blue{h(t)}\\[6pt] & = \red{CD}\left(\blue{\frac{f(t) - f(a)}{f(b) - f(a)} - \frac{g(t)-g(a)}{g(b)-g(a)}}\right)\\[6pt] & = \frac{\red{CD}\blue{(f(t) - f(a))}}{\blue{f(b) - f(a)}} - \frac{\red{CD}\blue{(g(t)-g(a))}}{\blue{g(b)-g(a)}}\\[6pt] & = \frac{\red{\Big(f(b)-f(a)\Big)\Big(g(b)-g(a)\Big)}\blue{\Big(f(t) - f(a)\Big)}}{\blue{f(b) - f(a)}} - \frac{\red{\Big(f(b)-f(a)\Big)\Big(g(b)-g(a)\Big)}\blue{\Big(g(t)-g(a)\Big)}}{\blue{g(b)-g(a)}}\\[6pt] & = \frac{\cancelred{\Big(f(b)-f(a)\Big)}\Big(g(b)-g(a)\Big)\Big(f(t) - f(a)\Big)}{\cancelred{\Big(f(b) - f(a)\Big)}} - \frac{\Big(f(b)-f(a)\Big)\cancelred{\Big(g(b)-g(a)\Big)}\Big(g(t)-g(a)\Big)}{\cancelred{\Big(g(b)-g(a)\Big)}}\\[6pt] & = \frac{\Big(g(b)-g(a)\Big)\Big(f(t) - f(a)\Big)}{1} - \frac{\Big(f(b)-f(a)\Big)\Big(g(t)-g(a)\Big)}{1}\\[6pt] & = \Big(g(b)-g(a)\Big)\Big(f(t) - f(a)\Big)\Big(f(b)-f(a)\Big)\Big(g(t)-g(a)\Big) \end{align*} $$
Like we did in the earlier proof, we show that $$ H $$ satisfies Rolle's Theorem. As before, continuity and differentiability are satisfied since $$ f $$ and $$ g $$ are both continuous and differentiable. Then, we show the endpoints are the same:
$$ \begin{align*} H(\blue a) & = \Big(g(b)-g(a)\Big)\overbrace{\Big(f(\blue a)-f(a)\Big)}^{\mbox{Equals 0}} - \Big(f(b)-f(a)\Big)\overbrace{\Big(g(\blue a)-g(a)\Big)}^{\mbox{Equals 0}}\\[6pt] & = \Big(g(b)-g(a)\Big)\cdot \blue 0 - \Big(f(b)-f(a)\Big)\cdot \blue 0\\[6pt] & = 0 \end{align*} $$
$$ \begin{align*} H(\red b) & = \Big(g(b)-g(a)\Big)\Big(f(\red b)-f(a)\Big) - \Big(f(b)-f(a)\Big)\Big(g(\red b)-g(a)\Big)\\[6pt] & = \underbrace{\Big(f(b)-f(a)\Big)\Big(g(b)-g(a)\Big)}_{\mbox{This term..}} - \underbrace{\Big(f(b)-f(a)\Big)\Big(g(b)-g(a)\Big)}_{\mbox{ is the same as this term.}}\\[6pt] & = 0 \end{align*} $$
Consequently, Rolle's Theorem tells us there is some $$ c\in(a,b) $$ where $$ H'(c)=0 $$. We find
$$ H'(t) = \Big[g(b)-g(a)\Big]f'(t) - \Big[f(b)-f(a)\Big]g'(t), $$
and since $$ H'(\blue c) = 0 $$ we have
$$ \begin{align*} f'(\blue c)[g(b)-g(a)] - g'(\blue c)[f(b)-f(a)] & = 0\\[6pt] f'(\blue c)[g(b)-g(a)] & = g'(\blue c)[f(b)-f(a)] \end{align*} $$
which is what we needed to show.
Practice Problems
Calculate $$ \Delta f $$ and $$ \Delta g $$ over $$ \left[0,\frac \pi 2 \right] $$.
$$ \begin{align*} \Delta f & = \blue{f\left(\frac\pi 2\right)} - \red{f(0)} = \blue{2\sin \frac \pi 2} - \red{2\sin 0} = \blue 2 - \red 0 = 2\\[6pt] \Delta g & = \blue{g\left(\frac \pi 2\right)} - \red{g(0)} = \blue{3\cos\frac\pi 2}-\red{3\cos 0} = \blue 0 - \red 3 = -3 \end{align*} $$
Calculate $$ k $$ so that $$ \blue{\Delta f} = k\cdot \red{\Delta g} $$.
$$ \begin{align*} \blue{\Delta f} & = k\cdot \red{\Delta g}\\ \blue 2 & = k(\red{-3})\\ k & = \frac{\blue 2}{\red{-3}} = -\frac 2 3 \end{align*} $$
Find $$ f' $$ and $$ g' $$.
$$ \begin{align*} f'(x) & = 2\cos x\\ g'(x) & = -3\sin x \end{align*} $$
Find the $$ x $$-value in $$ \left(0, \frac \pi 2\right) $$ where $$ f'(x) = k\cdot g'(x) $$ for $$ k = -\frac 2 3 $$ as found previously.
$$ \begin{align*} \blue{f'(x)} & = k\cdot \red{g'(x)}\\[6pt] \blue{2\cos x} & = \left(-\frac 2 3\right)\red{(-3\sin x)}\\[6pt] 2\cos x & = 2\sin x\\[6pt] \frac{2\cos x}{2\cos x} & = \frac{2\sin x}{2\cos x}\\[6pt] 1 & = \tan x\\[6pt] x & = \frac \pi 4 \end{align*} $$
Well, $$ x = \frac \pi 4 + n\pi $$ for integer values of $$ n $$. However, only $$ x = \frac \pi 4 $$ is in the interval.
$$x = \frac \pi 4$$
For reference, here is the graph of the two functions along with the tangent lines.

Calculate $$ \Delta f $$ and $$ \Delta g $$ over $$ \left[-\ln 9, \ln 4\right] $$.
$$ \begin{align*} \Delta f & = \blue{f(\ln 4)} - \red{f(-\ln 9)} = \blue{4e^{0.5(\ln 4)}} - \red{4e^{0.5(-\ln 9)}} = 4\left(e^{\ln(4^{0.5})} - e^{\ln 9^{-0.5}}\right)\\[6pt] & = 4\left(4^{1/2}) - 9^{-0.5}\right) = 4\left(\sqrt 4 - \frac 1 {\sqrt 9}\right) = 4\left(2 - \frac 1 3\right) = \frac{20} 3 \end{align*} $$
$$ \begin{align*} \Delta g & = \blue{g(\ln 4)} - \red{g(-\ln 9)} = \blue{\frac 2 5e^{-2\ln 4}} - \red{\frac 2 5e^{-2(-\ln 9)}} = \frac 2 5\left(e^{\ln 4^{-2}} - e^{\ln 9^2}\right)\\[6pt] & = \frac 2 5 \left(4^{-2} - 9^2\right) = \frac 2 5\left(\frac 1 {16} - 81\right) = \frac 2 5\left(-\frac{1295}{16}\right) = - \frac{259} 8 \end{align*} $$
Calculate the value of $$ k $$ so that $$ \Delta f = k\cdot \Delta g $$.
$$ \begin{align*} \blue{\Delta f} & = k\cdot \red{\Delta g}\\[6pt] \blue{\frac{20} 3} & = k\cdot\red{\left(-\frac{259} 8\right)}\\[6pt] k & = \blue{\frac{20} 3} \cdot \red{\left(-\frac 8 {259}\right)} = - \frac{160}{777} \end{align*} $$
Find $$ f'(x) $$ and $$ g'(x) $$.
$$ \begin{align*} f'(x) & = 2e^{0.5x}\\[6pt] g'(x) & = -\frac 4 5e^{-2x} \end{align*} $$
Find the value of $$ x \in (-\ln 9, \ln 4) $$ such that $$ f'(x) = k\cdot g'(x) $$.
$$ \begin{align*} \blue{f'(x)} & = k\cdot \red{g'(x)}\\[6pt] \blue{2e^{0.5x}} & = -\frac{160}{777}\cdot \red{\left(-\frac 4 5e^{-2x}\right)}\\[6pt] e^{0.5x} & = \frac{64}{777}\cdot e^{-2x}\\[6pt] e^{0.5x}\cdot e^{2x} & = \frac{64}{777}\\[6pt] e^{2.5x} & = \frac{64}{777}\\[6pt] 2.5x & = \ln\left(\frac{64}{777}\right)\\[6pt] \frac 5 2x & = \ln\left(\frac{64}{777}\right)\\[6pt] x & = \frac 2 5\ln\left(\frac{64}{777}\right) = 0.4\ln\left(\frac{64}{777}\right)\\[6pt] \end{align*} $$
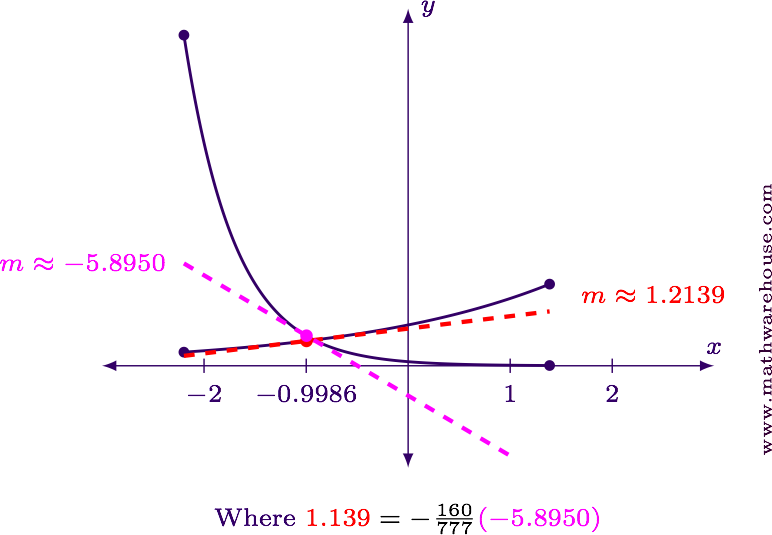
$$x = \frac 2 5\ln(64/777) \approx -0.9986$$
As ugly as it is, the answer is correct. Let's double-check our answer by showing $$ f'(x) = k\,g'(x) $$ at $$ x = 0.4\ln(64/777) $$ when $$ k = -160/777 $$.
First, we’ll find the values of the derivatives at the $$x$$-value we found.
$$ \begin{align*} f'(\red x) & = 2e^{0.5\red x}\\[6pt] f'\big(\red{0.4\ln(64/777)}\big) & = 2e^{0.5(\red{0.4\ln(64/777)})}\\[6pt] & = 2 e^{0.2\ln(64/777)}\\[6pt] & = 2 e^{(1/5)\ln(64/777)}\\[6pt] & = 2 e^{\ln(64/777)^{1/5}} & \text{Property of Logarithms}\\[6pt] & = 2 \cdot \left(\frac{64}{777}\right)^{1/5} & \text{Inverse Functions}\\[6pt] & \approx 1.2139 \end{align*} $$
$$ \begin{align*} g'(\red x) & = -\frac 4 5 e^{-2\red x}\\[6pt] g'\big(\red{0.4\ln(64/777)}\big) & = -\frac 4 5 e^{-2(\red{0.4\ln(64/777)})}\\[6pt] & = -\frac 4 5 e^{-0.8\ln(64/777)}\\[6pt] & = -\frac 4 5 e^{(-4/5)\ln(64/777)}\\[6pt] & = -\frac 4 5 e^{\ln(64/777)^{-4/5}} & \text{Property of Logarithms}\\[6pt] & = -\frac 4 5 \left(\frac{64}{777}\right)^{-4/5} & \text{Inverse Functions}\\[6pt] & \approx -5.8950 \end{align*} $$
Next, we show these values satisfy the equation $$ f' = kg' $$.
$$ \begin{align*} \blue{k}\,g'\big(0.4\ln(64/777)\big) & = \blue{-\frac{160}{777}}\left(-\frac 4 5 \cdot \left(\frac{64}{777}\right)^{-4/5}\right)\\[6pt] & = \frac{128}{777}\cdot \left(\frac{64}{777}\right)^{-4/5}\\[6pt] & = 2\left(\frac{64}{777}\right)^1\cdot \left(\frac{64}{777}\right)^{-4/5} & \text{Factor off a 2}\\[6pt] & = 2\left(\frac{64}{777}\right)^{1/5} & a^m\cdot a^n = a^{m+n}\\[6pt] & = f'\big(0.4\ln(64/777)\big) \end{align*} $$
For reference, here is the graph of the two functions, and the tangent lines.
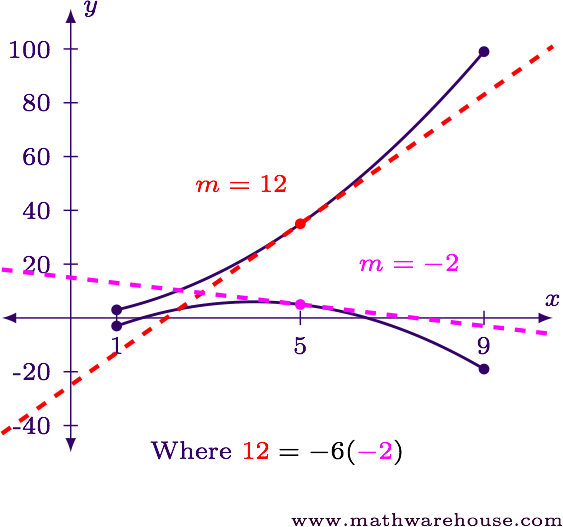
Find $$ f'(5) $$ and $$ g'(5) $$.
$$ \begin{align*} f'(x) & = 2x + 2\\[6pt] f'(5) & = 2(5) + 2 = 12\\[6pt] &\\ g'(x) & = -2(x-4)\\[6pt] g'(5) & = -2(5 -4) = -2 \end{align*} $$
Find the value of $$ k $$ so that $$ f'(5) = k\,g'(5) $$.
$$ \begin{align*} f'(5) & = k\,g'(5)\\[6pt] 12 & = k(-2)\\[6pt] k & = -6 \end{align*} $$
Find a formula $$ \Delta f $$ for $$ \Delta g $$ for the interval $$ [1,b] $$.
$$ \begin{align*} \Delta f & = \blue{f(b)} - \red{f(1)}\\[6pt] & = (\blue{b^2 + 2b}) - (\red{1^2 + 2(1)})\\[6pt] & = \blue{b^2 + 2b} - (\red{3})\\[6pt] & = b^2 + 2b - 3 \end{align*} $$
$$ \begin{align*} \Delta g & = \blue{g(b)} - \red{g(1)}\\[6pt] & = \blue{6 - (b-4)^2} - (\red{6 - (1-4)^2})\\[6pt] & = \blue{6 - (b-4)^2} - (\red{-3})\\[6pt] & = 9 - (b-4)^2 \end{align*} $$
Solve the equation $$ \Delta f = k\,\Delta g $$ using the formulas from Step 3 and the $$ k $$-value from Step 2.
$$ \begin{align*} \Delta f & = k\,\Delta g\\[6pt] b^2 + 2b - 3 & = -6\big[9 - (b-4)^2\big]\\[6pt] b^2 + 2b - 3 & = -54 +6(b-4)^2\\[6pt] b^2 + 2b - 3 & = -54 +6(b^2-8b +16)\\[6pt] b^2 + 2b - 3 & = 6b^2-48b + 42\\[6pt] 5b^2 - 50b + 45 & = 0\\[6pt] b^2 - 10b + 9 & = 0\\[6pt] (b - 9)(b-1) & = 0\\[6pt] b = 9 & \mbox{ and }b = 1 \end{align*} $$
Since the left endpoint of the interval is at $$ x = 1 $$, we know the right endpoint should be $$ b = 9 $$.
For reference, here is the graph of $$ f(x) $$ and $$ g(x) $$ along with the tangent lines.