Quick Overview
- With the MVT, we can prove the following ideas:
- If the derivative of a function is positive, then the function must be increasing.
- If the derivative of a function is negative, then the function must be decreasing.
- If the derivative of a function is zero, the function is constant.
- If two functions have the same derivative, then the two functions differ only by a con- stant.
- The exponential function is the only non-trivial function that is its own derivative.
In the previous lesson we included a quote about the Mean Value Theorem:
The following theorems are not really the “theorems of major significance” mentioned by Purcell and Varberg. In fact, they are rather simple ideas. However, as simple as they are to understand, they are difficult (or impossible) to prove unless we use the Mean Value Theorem.
More importantly, the proofs of these theorems can help you see how the MVT is used in mathematical proofs.
The Increasing (or Decreasing) Function Theorem
Basic Idea
If the derivative of a function is positive, then the function must be increasing. Similarly, if the derivative of a function is negative, then the function must be decreasing.
Formal Theorem Statement
Suppose $$f(x)$$ is continuous on the interval $$[a,b]$$, and differentiable on $$(a,b)$$, and $$f'(x) \geq 0$$ for all $$x\in(a,b)$$. Then $$f$$ is increasing on $$(a,b)$$.
Defining Increasing and Decreasing
Before we prove the theorem, we need to have a good definition for what we mean by an "increasing function" and a "decreasing function."
Suppose we pick two $$x$$-values in the interval $$[a,b]$$. Let's call them $$x_1$$ and $$x_2$$ so that $$x_1 < x_2$$. Then if $$f(x_1) \leq f(x_2)$$ no matter which $$x_1$$ and $$x_2$$ we choose, then we say $$f$$ is increasing on $$[a,b]$$.
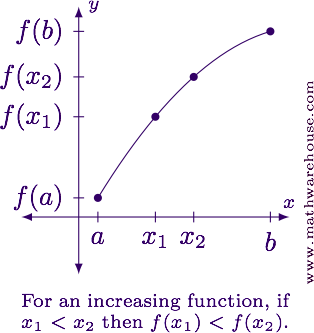
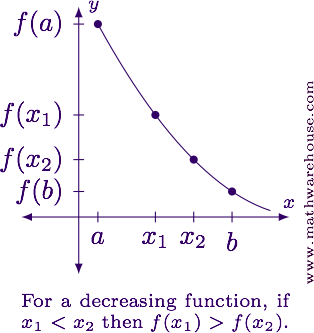
Similarly, if $$f(x_1) \geq f(x_2)$$ no matter which $$x_1$$ and $$x_2$$ we choose, then we say $$f$$ is decreasing on $$[a,b]$$.
Proof of the Theorem:
This theorem has three hypotheses: (1) continuity, (2) differentiability, and (3) $$f'(x)$$ is positive. The first two hypotheses allow us to use the Mean Value Theorem.
We'll use it this way: we can pick any $$x_1$$ and $$x_2$$ in $$(a,b)$$ where $$x_1 < x_2$$. Then the Mean Value Theorem guarantees we can find a $$c \in (x_1, x_2)$$ where
$$\frac{f(x_2) - f(x_1)}{x_2 - x_1} = f'(c).$$
If we multiply both sides of this equation by the denominator we get
$$f(x_2) - f(x_1) = f'(c)(x_2 - x_1)$$
Since the right-hand side is positive (do you see why?) we now know that
$$ \begin{align*} f(x_2) - f(x_1) & > 0\\ f(x_2) & > f(x_1). \end{align*} $$
So the function must be increasing. Since we can do this for any $$x_1$$, $$x_2$$ pair in $$(a,b)$$, the function must be increasing over the entire interval.
To prove that a function whose derivative is negative must be decreasing is shown similarly.
Only Constant Functions have $$f'(x) = 0$$ Everywhere
Basic Idea
We know that if we start with a constant function that it's derivative must be equal to zero. However, could we find (or invent) a function whose derivative is zero everywhere, but the function isn't constant? This theorem claims we can't, but we'll have to prove it.1
Formal Statement:
If $$f'(x) = 0$$ for all $$x\in (a,b)$$, then the function is constant over $$(a,b)$$.
Proof:
Since $$f'(x)$$ exists everywhere in $$(a,b)$$, we know the $$f$$ is both continuous and differentiable. That means we can use the Mean Value Theorem.
Like we did in the previous proof, we can pick any $$x_1, x_2\in (a,b)$$ such that $$x_1 < x_2$$. So
$$a < x_1 < x_2 < b.$$
The MVT guarantees there is a $$c\in (x_1,x_2)$$ where
$$ \frac{f(x_2) - f(x_1)}{x_2 - x_1} = f'(c), $$
and since $$f'(c) = 0$$ we know
$$f(x_2) - f(x_1) = 0.$$
But then $$f(x_1) = f(x_2)$$. Since this is true for any $$x_1$$, $$x_2$$ pair we pick, the function is constant.
1While this seems 'obvious', you need to understand that in math there are some really bizarre functions that have been created. So proving even `obvious' ideas helps us know what can and can't actually be done in mathematics.
Suppose Two Functions Have the Same Derivative
Basic Idea
Suppose two functions have the exact same derivative (like the ones shown below).
Then the two functions must be essentially the same function. In fact, they will only differ by a constant.

Formal Statement
Suppose $$f'(x) = g'(x)$$. Then $$f(x) = g(x) + k$$.
Proof:
This proof relies on the previous theorem rather than on the MVT directly.
We start with the assumption that we have two functions, $$f(x)$$ and $$g(x)$$, and the only thing we know about them is that their derivatives are equal for all $$x$$ in their domain.
Next, we'll define a new function that is based on $$f$$ and $$g$$. Specifically, we'll let
$$ h(x) = f(x) - g(x). $$
Since $$f$$ and $$g$$ are both differentiable we know our new function is too, and in fact
$$ h'(x) = f'(x) - g'(x). $$
Now, our basic assumption for this theorem is that $$f'(x) = g'(x)$$ which means $$f'(x) - h'(x) = 0$$. But that means $$h'(x) = 0$$ everywhere.
The previous theorem we proved tells us $$h(x)$$ must be constant. That is, $$h(x) = k$$, which implies $$f(x) - g(x) = k$$ which means $$f(x) = g(x) + k$$.
Uniqueness of the Exponential Function
Basic Idea
The claim is that there is only one function that is equal to its own derivative: $$f(x) = a\,e^x$$, where $$a$$ is any constant.
Formal Statement
The function $$f(x) = ae^x$$ is the only non-trivial function where $$f = f'$$ for all $$x$$.
Note: The `trivial function' referred to in the statement is the horizontal line $$y = 0$$.
Proof:
As before, this proof relies indirectly on the Mean Value Theorem. Instead, it utilizes one of our previous theorems: A function whose derivative is $$0$$ everywhere must be a constant function.
We start by assuming there could be a second function that is equal to its own derivative. Let's call it $$g$$, so $$g = g'$$.
Now, let's define a new function.
$$ h(x) = \frac{f(x)}{g(x)} $$
If we find the derivative of $$h$$ we get
$$ h'(x) = \frac{g(x)\cdot f'(x) - f(x)\cdot g'(x)}{[g(x)]^2}. $$
Since $$\blue{f = f'}$$ and $$\red{g = g'}$$, we make a replacement in $$h'(x)$$.
$$ \begin{align*} h'(x) & = \frac{g(x)\cdot \blue{f'(x)} - f(x)\cdot \red{g'(x)}}{[g(x)]^2}\\[6pt] & = \frac{\blue{f(x)}g(x) - f(x)\red{g(x)}}{[g(x)]^2}\\[6pt] &= 0 \end{align*} $$
This means (again by the previous theorem) that $$h(x)$$ is constant. So
$$ \begin{align*} h(x) & = k\\[6pt] \frac{f(x)}{g(x)} & = k\\[6pt] f(x) & = kg(x) \end{align*} $$
which means $$g(x)$$ is just a scaled version of $$f(x)$$. Thus, only the exponential function is its own derivative.
















