Quick Overview
- The derivative is the main tool of Differential Calculus.
- Specifically, a derivative is a function...
- that tells us about rates of change, or...
- slopes of tangent lines.
- Its definition involves limits.
The Derivative is a Function
Suppose we have a particular function:
$$f(x) =2x^5+7x^3+5$$
Through a process called differentiation1 we can find another function that's related to $$f$$. This second function is called the derivative of $$f$$. For this example, the derivative is:
$$f'(x) = 10x^4 + 21x^2$$
1Differentiation means finding the derivative.
Two Notations for the Derivative

The Derivative Tells Us About Rates of Change
Example 1
Suppose $$D(t)$$ is a function that measures our distance from home (in miles) as a function of time (in hours).
Then $$D(2) = 5$$ means you are 5 miles from home after 2 hours have elapsed,
and $$D'(2) = 20$$ tells us that after 2 hours have elapsed...
$$ \frac{\mbox{our distance is changing 20 miles...}}{\mbox{for each hour that passes.}} = \frac{\mbox{20 miles}}{\mbox{each hour}} = 20\mbox{ miles per hour.} $$
So $$D'(2) = 20$$ is telling us that after 2 hours have elapsed our velocity is 20 miles per hour.
Example 2
Suppose $$C(x)$$ is the cost (in dollars) of producing $$x$$ tons of macaroni.
Then $$C(30) = 15{,}000$$ tells us that producing 30 tons of macaroni will cost $15,000,
and $$C'(30) = 48{,}000$$ tells us that when we are producing 30 tons of macaroni, the associated costs are increasing at a rate of $48,000 per ton.
The Derivative Tells Us About Slopes of Tangent Lines
Let's take another look at the Leibnitz notation for the derivative. If $$y = f(x)$$ is our function then the derivative can be notated as
$$\frac{dy}{dx} = \frac{\mbox{change in \(y\)}}{\mbox{change in \(x\)}} = \mbox{the slope of a line!}$$
Derivative values are the slopes of lines. Specifically, they are slopes of lines that are tangent to the function. See the example below.
Example 3
Suppose we have a function2 where $$f(2) = 3$$ and $$f'(2) = 1$$. The first equation tells us the point $$(2,3)$$ is on the graph of the function. The second equation tells us the slope of the tangent line passing through this point.
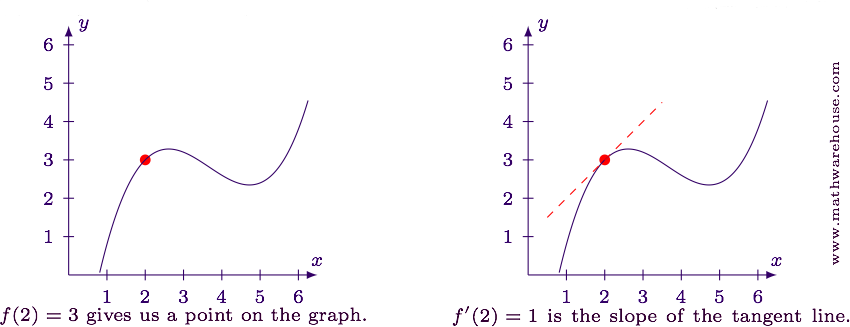
Just like a slope tells us the direction a line is going, a derivative value tells us the direction a curve is going at a particular spot. At each point on the graph, the derivative value is the slope of the tangent line at that point.
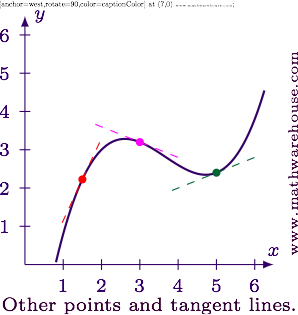
2In case you're wondering, I'm using the function $$f(x) = 3 + (x-2) - (x-2)^2 + \frac 1 5(x-2)^3$$.
Definition of the Derivative
Suppose we have a function, $$f(x)$$, and we want to find the derivative. How can we do that? The most basic way is to use the definition of the derivative:
$$f'(x) = \displaystyle\lim_{h\to 0} \frac{f(x+h) - f(x)} h$$
Variations of the Definition
There are two popular variations of the above definition. They are mathematically equivalent to the one given above.
- $$\displaystyle f'(x) = \lim_{\Delta x \to 0} \frac{f(x+\Delta x) - f(x)}{\Delta x}$$
- $$\displaystyle f'(x) = \lim_{x\to a} \frac{f(x) - f(a)}{x-a}$$
In the next lesson, we'll practice differentiating functions using the definition of the derivative.














