Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to 0^+} \blue{x}\,\red{\ln x} = \blue 0 (\red{-\infty}) $$
Determine which form ($$ 0/0 $$ or $$ \infty/\infty $$) to use.
-
Choice 1: Move the $$ x $$.
Thinking ahead: The derivative of logarithm is just $$ 1/x $$ which gets rid of the logarithm in our calculations.
-
Choice 2: Move the natural log.
Thinking ahead: The reciprocal of the natural log is $$ (\ln x)^{-1} $$, whose derivative involves a $$ (\ln x)^{-2} $$. Yuck.
Based on our thinking ahead, let's use Choice 1 and move the $$ x $$.
Rewrite the limit and re-evaluate.
$$ \displaystyle\lim_{x\to 0^+} \blue{x}\,\ln x = \lim_{x\to 0^+} \frac{\ln x}{\blue{1/x}} = \frac{-\infty}{\blue{\infty}} $$
Apply L'Hôpital's rule, simplify, and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 0^+} \frac{\ln x}{1/x} & = \lim_{x\to 0^+} \frac{\blue{\frac d {dx}\left(\ln x\right)}}{\red{\frac d {dx}\left(x^{-1}\right)}}&& \href{what-is-Lhopitals-rule.php}{\text{L'Hôpital's rule}}\\[6pt] & = \lim_{x\to 0^+} \frac{\blue{1/x}}{\red{-x^{-2}}}\\[6pt] & = \lim_{x\to 0^+} \frac{1/x}{-1/x^2} &&\mbox{Simplifying}\\[6pt] & = \lim_{x\to 0^+} \frac 1 x\,\left(-\frac{x^2} 1\right)\\[6pt] & = \lim_{x\to 0^+} -x\\[6pt] & = 0 && \text{Re-evaluating the limit.} \end{align*} $$
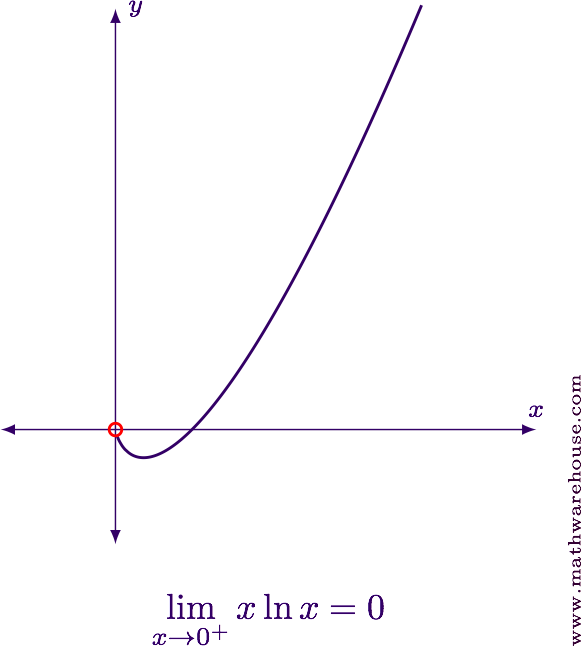
$$\displaystyle \lim_{x\to 0^+} x\ln x = 0$$
For reference, here is the graph of the function and the limit value.
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to \infty} \blue x\cdot\red{\arccot x} = \blue \infty \cdot \red 0 $$
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Move the $$ \arccot x $$.
Thinking ahead: We would need to find the derivative of $$ (\arccot x)^{-1} $$, which will be a bit messy.
-
Choice 2: Move the $$ x $$.
Thinking ahead: The derivative of $$ \arccot x $$ is easy, and the derivative of $$ 1/x $$ is too.
Choice 2 seems a little more straightforward.
Rewrite the limit and re-evaluate.
$$ \displaystyle\lim_{x\to \infty} \blue x\,\arccot x = \displaystyle\lim_{x\to \infty} \frac{\arccot x}{\blue{1/x}}\\[6pt] = \frac 0 0\\[6pt] $$
Apply L'Hôpital's rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to \infty} \frac{\arccot x}{1/x} & = \lim_{x\to \infty} \frac{\red{\frac d {dx}\left(\arccot x\right)}}{\blue{\frac d {dx}\left(x^{-1}\right)}}\\[6pt] & = \lim_{x\to \infty} \frac{\red{\frac{-1}{1 + x^2}}}{\blue{-x^{-2}}}\\[6pt] & = \lim_{x\to \infty} \red{\frac{-1}{1 + x^2}}\cdot \blue{\frac 1 {-x^{-2}}} & \text{Simplifying}\\[6pt] & = \lim_{x\to \infty} \frac{-1}{1 + x^2}\cdot \frac{x^2} 1\\[6pt] & = \lim_{x\to \infty} \frac{x^2}{1 + x^2}\\[6pt] & = 1 \end{align*} $$
Technically, we could use L'Hôpital's rule twice more on that final limit, but the rule really just tells us to compare how quickly the numerator and denominator are changing. In this case, they are both changing quadratically, and have the same coefficient, so they will balance out as $$ x $$ grows infinitely large.
If you need to show "work", you could impress them by recalling the limit techniques from earlier (see Limits at Infinity---Rational Forms).
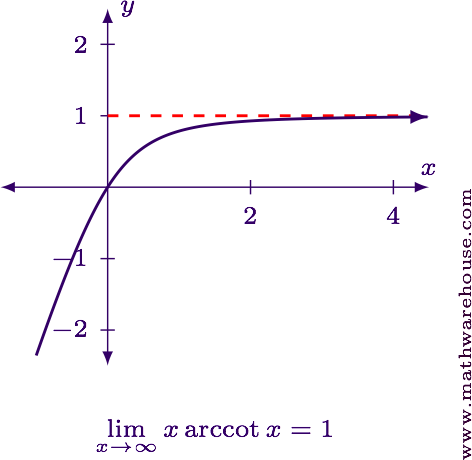
$$\displaystyle \lim_{x\to \infty} x\arccot x = 1$$
For reference, here is the graph of the function.
Evaluate the limit in its current form.
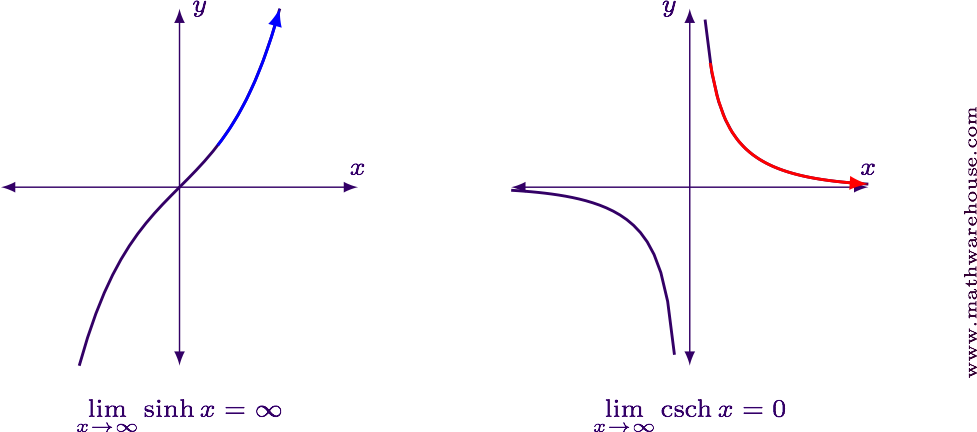
Note that $$ \displaystyle \csch x = \frac 1 {\sinh x} $$ and we know $$ \displaystyle \lim_{x\to\infty} \sinh x = \infty $$. Consequently, $$ \displaystyle \lim_{x\to\infty} \csch x = 0 $$. (See the graphs below).
So our limit currently has the form
$$ \displaystyle\lim_{x\to\infty} \blue x\,\red{\csch x} = \blue \infty \cdot \red{0} $$
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Move the $$ \csch x $$.
Thinking ahead: $$ \frac 1 {\csch x} = \sinh x $$ the derivative of which is simple.
-
Choice 2: Move the $$ x $$.
Thinking ahead: The derivative of the $$ \csch x $$ is a bit messy.
Choice 1 seems much simpler, so let's start there.
Rewrite the limit and re-evaluate.
$$ \begin{align*} \lim_{x\to\infty} x\,\red{\csch x} & = \lim_{x\to\infty} \frac x {\red{1/\csch x}} = \lim_{x\to\infty} \frac x {\red{\sinh x}} = \lim_{x\to\infty} \frac \infty \infty \end{align*} $$
Use L'Hôpital's rule and then re-evaluate the limit.
$$ \begin{align*} \lim_{x\to\infty} \frac{x}{\sinh x} & = \lim_{x\to\infty} \frac{\blue{\frac d {dx} (x)}}{\red{\frac d {dx}(\sinh x)}} = \lim_{x\to\infty} \frac{\blue 1}{\red{\cosh x}} = \frac 1 \infty = 0 \end{align*} $$
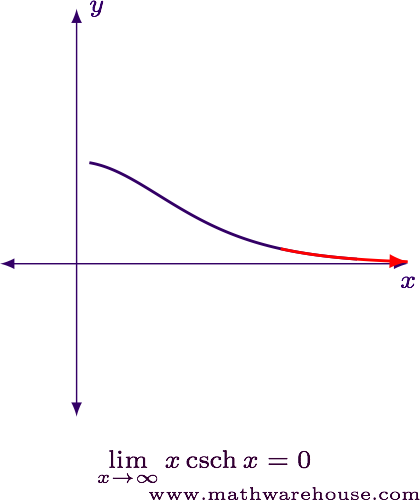
$$ \displaystyle \lim_{x\to \infty} x\csch x = 0 $$
For reference, below is a graph of the function.
Evaluate the limit in its current form.
We know from the graph of $$ y = \csch x $$ that $$ \displaystyle \lim_{x\to 0} \csch x = \pm \infty $$.
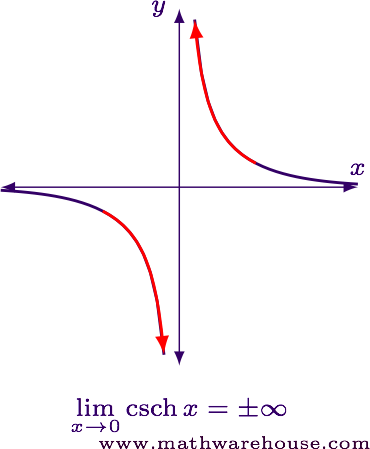
So our limit currently has the form
$$ \displaystyle\lim_{x\to\infty} \blue x\,\red{\csch x} = \blue 0 \cdot \red{(\pm \infty)} $$
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Move the $$ \csch x $$.
Thinking ahead: $$ \frac 1 {\csch x} = \sinh x $$. Its derivative is is $$ \cosh x $$.
-
Choice 2: Move the $$ x $$.
Thinking ahead: The derivative of $$ \csch x $$ is a bit messy.
Choice 1 seems simpler, so let's start there.
Rewrite the limit and re-evaluate.
$$ \displaystyle\lim_{x\to0} x\,\red{\csch x} = \displaystyle\lim_{x\to0} \frac x {\red{1/\csch x}} = \displaystyle\lim_{x\to0} \frac x {\red{\sinh x}} = \frac 0 {\sinh 0} = \frac 0 0 $$
Apply L'Hôpital's rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to0} \frac x {\sinh x} & = \lim_{x\to0} \frac{\blue{\frac d {dx}(x)}}{\red{\frac d {dx}\left(\sinh x\right)}}\\[6pt] & = \lim_{x\to0} \frac{\blue 1}{\red{\cosh x}}\\[6pt] & = \frac 1 {\cosh 0}\\[6pt] & = \frac 1 1\\[6pt] & = 1 \end{align*} $$
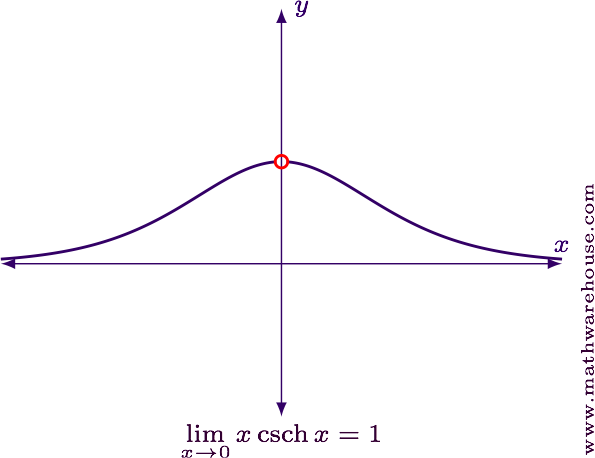
$$ \displaystyle \lim_{x\to 0} x\csch x = 1 $$
For reference, here is a graph of the function and the limit point.
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to\infty} \blue x\,\red{\tan\left(\frac 4 x\right)} = \blue \infty\cdot \red{\tan\left(\frac 4 \infty\right)} = \blue \infty\cdot \red{\tan 0} = \blue 0\,\red \infty $$
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Adjust the tangent.
Thinking ahead: The reciprocal of the tangent is a cotangent, so the derivative is easy. The derivative of $$ x $$ is 1.
-
Choice 2: Adjust the $$ x $$.
Thinking ahead: The derivative of tangent is easy. The derivative of $$ 1/x $$ is $$ -1/x^2 $$.
Both ways seem reasonable, so it might not matter which we choose, but Choice 1 seems a little simpler because of the derivatives of $$ x $$. So let's try Choice 1.
Rewrite the limit and re-evaluate.
$$ \begin{align*} \lim_{x\to\infty} x\,\red{\tan\left(\frac 4 x\right)} & = \lim_{x\to\infty} \frac x {\red{1/\tan\left(\frac 4 x\right)}}\\[6pt] & = \lim_{x\to\infty} \frac x {\red{\cot\left(\frac 4 x\right)}} \end{align*} $$
As $$ x $$ grows larger, $$ 4/x $$ approaches zero, but since $$ x $$ is positive, $$ 4/x $$ approaches zero from above. Understanding this allows us to evaluate
$$ \displaystyle\lim_{x\to\infty} \frac x {\cot\left(\frac 4 x\right)} = \frac \infty {\cot\left(0^+\right)} = \frac \infty \infty $$
where I'm using the $$ 0^+ $$ in the cotangent to indicate we're approaching 0 with positive values only.
Use L'Hôpital's rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to\infty} \frac x {\cot\left(\frac 4 x\right)} & = \lim_{x\to\infty} \frac{\blue{\frac d {dx}(x)}}{\red{\frac d {dx}\left(\cot\left(4x^{-1}\right)\right)}}\\[6pt] & = \lim_{x\to\infty} \frac{\blue 1}{\red{-\csc^2\left(4x^{-1}\right)(-4x^{-2})}} & \href{what-is-Lhopitals-rule.php}{\text{L'Hôpital's rule}}\\[6pt] & = \lim_{x\to\infty} \frac{x^2}{4\csc^2\left(\frac 4 x\right)} & \text{Simplified}\\[6pt] & = \frac \infty \infty \end{align*} $$
We can always try L'Hôpital's rule again, but I suspect we made a bad choice in using this form. Compare the function before and after we used L'Hôpital's rule:
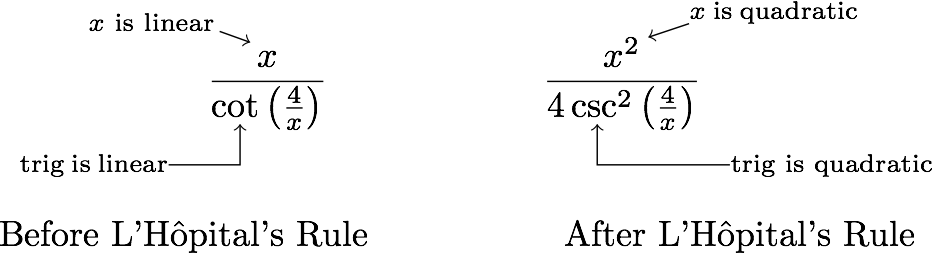
The fact that the powers on both the $$ x $$ term and the trigonometric function have increased makes it seem like we're going backwards, away from a solution.
Let's go ahead and peak at what would happen with a second application of L'Hôpital's rule:
$$ \begin{align*} \lim_{x\to\infty} \frac{x^2}{4\csc^2\left(4x^{-1}\right)} & = \lim_{x\to\infty} \frac{2x}{-8\csc^2\left(4x^{-1}\right)\cot\left(4x^{-1}\right)(-4x^{-2})} & \href{what-is-Lhopitals-rule.php}{\text{L'Hôpital's rule}}\\[6pt] & = \lim_{x\to\infty} \frac{x^3}{16\csc^2\left(4x^{-1}\right)\cot\left(4x^{-1}\right)} & \text{Simplified} \end{align*} $$
Notice our $$ x $$ term is now cubed, and the trig functions are getting messier.
One of the reasons this particular exercise was included on this website was to show you that sometimes you make a reasonable choice based on the information you have, and it still goes wrong. It's not a big deal. We just back up and try again using the other choice from Step 2.
Try Choice 2. Rewrite the original limit by moving the $$ x $$.
$$ \displaystyle\lim_{x\to\infty} \blue x\,\tan\left(\frac 4 x\right) = \displaystyle\lim_{x\to\infty} \frac{\tan\left(\frac 4 x\right)}{\blue{1/x}} = \frac{\tan 0} 0 = \frac 0 0 $$
Apply L'Hôpital's rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to\infty} \frac{\tan\left(\frac 4 x\right)}{1/x} & = \lim_{x\to\infty} \frac{\blue{\frac d {dx}\left[\tan\left(4 x^{-1}\right)\right]}}{\red{\frac d {dx}\left(x^{-1}\right)}}&& \href{what-is-Lhopitals-rule.php}{\text{L'Hôpital's rule}}\\[6pt] & = \lim_{x\to\infty} \frac{\blue{\sec^2\left(4 x^{-1}\right)\cdot(-4x^{-2})}}{\red{-x^{-2}}}\\[6pt] & = \lim_{x\to\infty} \frac{4\cancelred{x^{-2}}\,\sec^2\left(4 x^{-1}\right)}{\cancelred{x^{-2}}} && \text{Simplifying}\\[6pt] & = \lim_{x\to\infty} 4\sec^2\left(\frac 4 x\right)\\[6pt] & = 4\sec^2(0)\\[6pt] & = 4 \end{align*} $$
Nice! The factors of $$ x $$ canceled out completely!
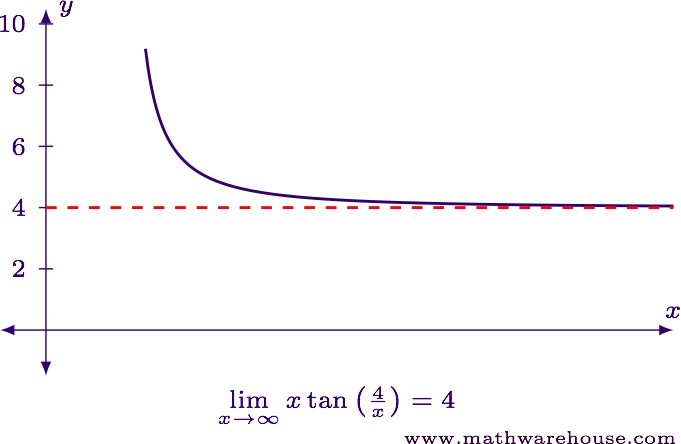
$$ \displaystyle \lim_{x\to\infty} x\tan\left(\frac 4 x\right) = 4 $$
For reference, the right-hand part of the graph of the function is shown with its horizontal asymptote.
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to 0^+} \blue{x^3}\,\red{e^{1/x}} = \blue{0^3}\cdot \red{e^{1/0}} = 0\cdot e^\infty = 0\cdot \infty $$
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Adjust the $$ e^{1/x} $$.
Thinking ahead: The derivative of $$ x^3 $$ is simple. And $$ 1/e^{1/x} = e^{-x^{-1}} $$ the derivative of which will produce factors of $$ x^{-2} $$ from the chain rule.
-
Choice 2: Adjust the $$ x^3 $$.
Thinking ahead: The derivative of $$ e^{1/x} $$ will produce a factor of $$ -x^{-2} $$ from the chain rule, while the reciprocal $$ x^{-3} $$ is straightforward to work with.
Choice 1 might seem more straightforward, but we'll run into problems with the power of $$ x $$. In Choice 2 the simplifications should work to reduce the power on $$ x $$.
Rewrite the limit in $$ \frac \infty \infty $$ form.
$$ \begin{align*} \lim_{x\to 0^+} \blue{x^3}\,e^{1/x} & = \lim_{x\to 0^+} \frac{e^{1/x}}{\blue{1/x^3}}\\[6pt] & = \frac{e^\infty}{1/0}\\[6pt] & \frac \infty \infty \end{align*} $$
Apply L'Hôpital's rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 0^+} \frac{e^{1/x}}{1/x^3} & = \lim_{x\to 0^+} \frac{\red{\frac d {dx} \left(e^{x^{-1}}\right)}}{\blue{\frac d {dx}\left(x^{-3}\right)}}\\[6pt] & = \lim_{x\to 0^+} \frac{\red{e^{x^{-1}}\cdot \left(-x^{-2}\right)}}{\blue{-3x^{-2}}}\\[6pt] & = \lim_{x\to 0^+} \frac{e^{x^{-1}}\cdot \cancelred{\left(-x^{-2}\right)}}{3\cdot \cancelred{\left(-x^{-2}\right)}}\\[6pt] & = \lim_{x\to 0^+} \frac{e^{x^{-1}}} 3\\[6pt] & = \frac 1 3 e^{1/0}\\[6pt] & = \infty \end{align*} $$
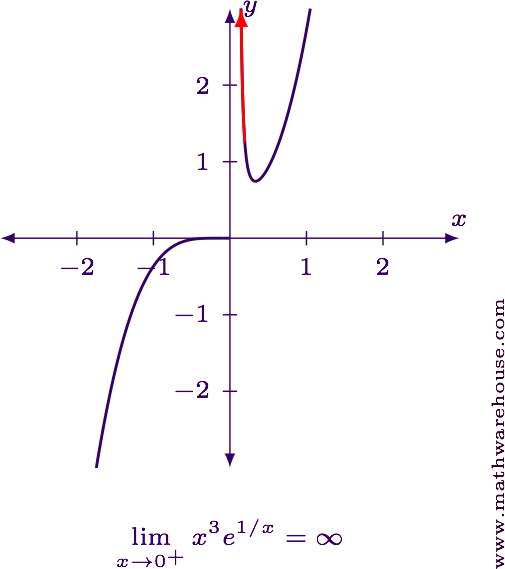
$$ \displaystyle \lim_{x\to 0^+} x^3 e^{1/x} = \infty $$
For reference, here is the graph of the function.
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to0^+} \blue{\ln x}\,\red{\sin x} = \blue{-\infty}\cdot \red 0 $$
Determine which form ($$ 0/0 $$ or $$ \infty/\infty $$) to use.
-
Choice 1: Leave the natural log alone, and move the $$ \sin x $$.
Thinking ahead: The derivative of the logarithm is just $$ 1/x $$, which gets rid of the logarithm from our computations. The reciprocal of the sine is a cosecant whose derivative is pretty straightforward.
-
Choice 2: Move the natural log, leave the sine alone.
Thinking ahead: The derivative of the sine is just a cosine. Easy. But the reciprocal of the natural log is $$ 1/(\ln x) = (\ln x)^{-1} $$, the derivative of which involves a $$ (\ln x)^{-2} $$.
Choice 1 seems the better choice.
Rewrite the limit and re-evaluate.
$$ \displaystyle\lim_{x\to0^+} \ln x\,\red{\sin x} = \displaystyle\lim_{x\to0^+} \frac{\ln x}{\red{1/\sin x}} = \displaystyle\lim_{x\to0^+} \frac{\ln x}{\red{\csc x}} = \frac{\ln 0^+}{\csc 0^+} = \frac{-\infty}{\infty} $$
Apply L'Hôpital's rule, simplify, and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to0^+} \frac{\ln x}{\csc x} & = \lim_{x\to0^+} \frac{\blue{\frac d {dx}\left(\ln x\right)}}{\red{\frac d {dx}\left(\csc x\right)}}& \href{what-is-Lhopitals-rule.php}{\text{L'Hôpital's rule}}\\[6pt] & = \lim_{x\to0^+} \frac{\blue{1/x}}{\red{-\csc x\cot x}}\\[6pt] & = \lim_{x\to0^+} \blue{\frac 1 x}\cdot \red{\left(-\frac 1 {\csc x}\right)\cdot \left(\frac 1 {\cot x}\right)} &\mbox{Simplifying}\\[6pt] & = \lim_{x\to0^+} \blue{\frac 1 x}\cdot \red{\left(-\sin x\right)\cdot \left(\cot x \right)}\\[6pt] & = \lim_{x\to0^+} -\frac 1 x\cdot\sin x\tan x \\[6pt] & = \lim_{x\to0^+} -\frac{\sin x} x\cdot\tan x\\[6pt] & = -\left(\lim_{x\to0^+} \frac{\sin x} x\right)\left(\lim_{x\to0^+} \tan x\right)\\[6pt] & = -1\cdot 0\\[6pt] & = 0 \end{align*} $$
Note: In an earlier lessons we showed $$ \displaystyle \lim_{x\to0}\frac{\sin x} x = 1 $$. Alternatively, we could use L'Hôpital's rule on $$ \lim\limits_{x\to 0^+}\frac{\sin x} x $$ since it is a $$ \frac 0 0 $$ form.
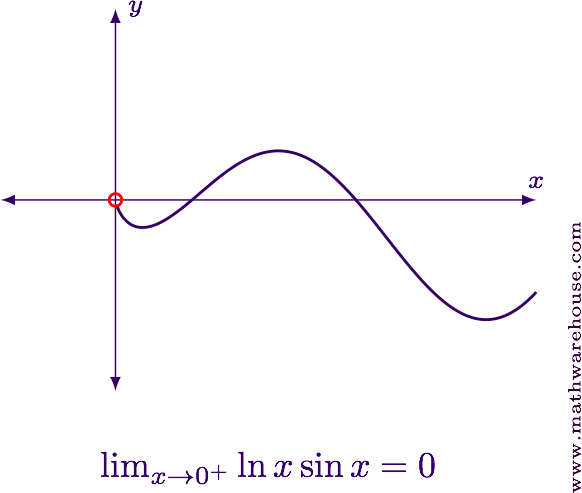
$$ \displaystyle \lim_{x\to0^+} \ln x\sin x = 0 $$
For reference, the graph of the function and the limit value is shown below.
Evaluate the limit in its current form.
Examining the individual graphs of the two factors, we see that $$ \blue{\sinh x \to 0} $$ and $$ \red{\ln x^2\to -\infty} $$ as $$ x\to 0 $$.
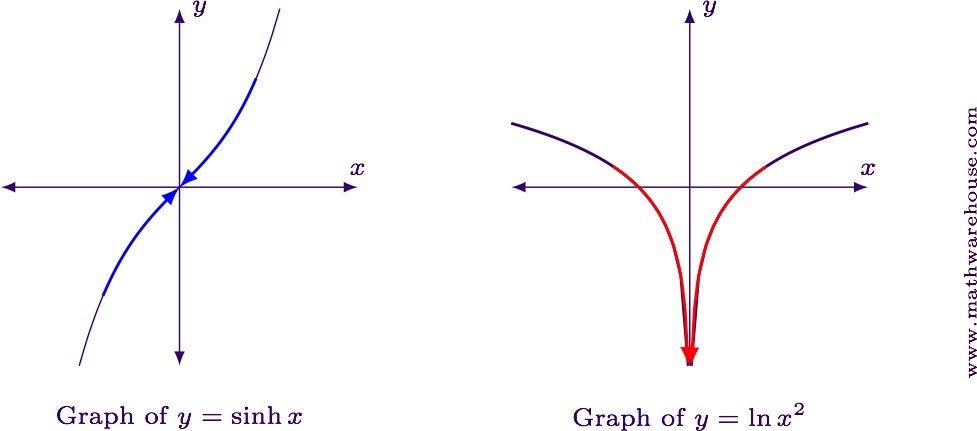
Consequently, $$ \displaystyle \lim_{x\to 0} \blue{\sinh x}\cdot \red{\ln x^2} = \blue 0\cdot \red{(-\infty)} $$.
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Adjust the natural log.
Thinking ahead: The derivative of $$ \sinh x $$ is easy enough, but the derivative of the adjusted natural log would involve a $$ \left(\ln x^2\right)^{-2} $$.
-
Choice 2: Adjust the hyperbolic sine.
Thinking ahead: The derivative of $$ \ln x^2 $$ is simple. The reciprocal of the $$ \sinh x $$ is just $$ \csch x $$.
At the outset, it looks like Choice 2 is the better option. Let's work with that one.
Adjust the function and re-evaluate the limit.
$$ \displaystyle\lim_{x\to 0} \blue{\sinh x}\cdot \ln x^2 = \displaystyle\lim_{x\to 0} \frac{\ln x^2}{\blue{1/\sinh x}} = \displaystyle\lim_{x\to 0} \frac{\ln x^2}{\blue{\csch x}} = \displaystyle\lim_{x\to 0} \frac{\ln 0}{\csch 0} = \frac{-\infty} \infty $$
Use L'Hôpital's rule. Simplify and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 0} \frac{\ln x^2}{\csch x} & = \lim_{x\to 0} \frac{\blue{\frac d {dx}\left(\ln x^2\right)}}{\red{\frac d {dx}\left(\csch x\right)}}\\[6pt] & = \lim_{x\to 0} \frac{\blue{2/x}}{\red{-\csch x\coth x}}\\[6pt] & = \lim_{x\to 0} -\frac{2\sinh x\tanh x} x && \text{Simplified}\\[6pt] & = -\frac{2\sinh 0\,\tanh 0} 0\\[6pt] & = -\frac{2(0)(0)} 0\\[6pt] & = \frac 0 0 \end{align*} $$
Another indeterminate form! Let's use L'Hôpital's rule a second time.
Use L'Hôspital's rule a second time. Simplify and re-evaluate
Notice that the numerator will require the product rule if we just plow ahead with L'Hôpital's rule. But we can save ourselves a little bit of work if we carefully use our properties of limits.
$$ \begin{align*} \lim_{x\to 0} -\frac{2\sinh x\tanh x} x & = -2\,\lim_{x\to 0}\left(\frac{\sinh x} x \cdot \tanh x\right)\\[6pt] & = -2\,\left(% \lim_{x\to 0} \frac{\sinh x} x \right) \cdot \left(\blue{\lim_{x\to 0} \tanh x}\right) && \text{Properties of Limits}\\[6pt] & = -2\,\left(% \lim_{x\to 0} \frac{\sinh x} x \right) \cdot \blue 0 \end{align*} $$
Now, $$ \lim\limits_{x\to 0} \frac{\sinh x} x = \frac 0 0 $$, so we can use L'Hôpital's rule for it.
$$ \begin{align*} -2\,\left(\lim_{x\to 0} \frac{\blue{\frac d {dx}\left(\sinh x\right)}}{\red{\frac d {dx}(x)}}\right) \cdot 0 & = -2\,\left(\lim_{x\to 0} \frac{\blue{\cosh x}}{\red 1}\right) \cdot 0\\[6pt] & = -2\,\left(\frac{\cosh 0} 1\right) \cdot 0\\[6pt] & = -2\,\left(\frac 1 1\right) \cdot 0\\[6pt] & = 0 \end{align*} $$
$$\displaystyle \lim_{x\to 0} \sinh x\cdot \ln x^2 = 0$$
For reference, here is the graph of the function and the limit value.
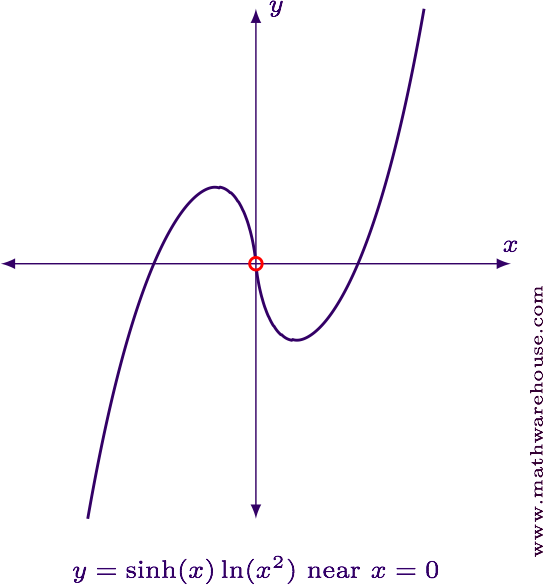
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to 0^+} \blue{\tanh x}\cdot \red{\ln x} = \blue{0}\cdot \red{(-\infty)} $$
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Adjust the natural log.
Thinking ahead: The derivative of $$ \tanh x $$ is straightforward, while the derivative of $$ (\ln x)^{-1} $$ is a bit more messy.
-
Choice 2: Adjust the hyperbolic tangent.
Thinking ahead: The derivative of the natural log is simple. The reciprocal of $$ \tanh x $$ is $$ \coth x $$, the derivative of which is simple enough.
Choice 2 seems to have the easiest derivative forms to work with, so let's start there.
Rewrite the function and re-evaluate the limit.
$$ \displaystyle\lim_{x\to 0^+} \blue{\tanh x}\cdot \ln x = \displaystyle\lim_{x\to 0^+} \frac{\ln x}{\blue{1/\tanh x}} = \displaystyle\lim_{x\to 0^+} \frac{\ln x}{\blue{\coth x}} = \frac{-\infty}{\infty} $$
Apply L'Hôpital's Rule, simplify and re-evaluate.
$$ \begin{align*} \lim_{x\to 0^+} \frac{\ln x}{\coth x} & = \lim_{x\to 0^+} \frac{\blue{\frac d {dx}\left(\ln x\right)}}{\red{\frac d {dx}\left(\coth x\right)}}\\[6pt] & = \lim_{x\to 0^+} \frac{\blue{1/x}}{\red{-\csch^2 x}}\\[6pt] & = \lim_{x\to 0^+} \frac{-\sinh^2 x} x && \text{Simplifying}\\[6pt] & = \lim_{\blue{x\to 0^+}} \left(-\sinh \blue x\cdot \frac{\sinh \blue x}{\blue x}\right)\\[6pt] & = -\sinh \blue 0\cdot \frac{\sinh \blue 0}{\blue 0}\\[6pt] & = 0\cdot \frac 0 0 \end{align*} $$
Apply L'Hôpital's rule a second time. Simplify and re-evaluate the limit.
Note that we only need to apply L'Hôpital's rule to the $$ \frac{\sinh x} x $$ part of the limit.
$$ \begin{align*} \lim_{x\to 0^+} \left(% -\sinh x\cdot \frac{\sinh x} x \right) & = \left(% \lim_{x\to 0^+} -\sinh x \right)\, \left(% \lim_{x\to 0^+}\frac{\sinh x} x \right) \text{Properties of Limits}\\[6pt] & = \left(-\sinh 0\right)\, \left(% \lim_{x\to 0^+} \frac{% \blue{\frac d {dx}\left(\sinh x\right)} } {% \red{\frac d {dx}(x)} } \right)\\[6pt] & = \left(0\right)\, \left(% \lim_{x\to 0^+} \frac{% \blue{\cosh x} } { \red{1} } \right)\\[6pt] & = \left(0\right)\, \left(% \frac{\cosh 0} 1 \right)\\[6pt] & = \left(0\right)\, \left(% \frac 1 1 \right)\\[6pt] & = 0 \end{align*} $$
$$ \displaystyle \lim_{x\to 0^+} \tanh x\cdot \ln x = 0 $$
For reference, here is the graph of the function and the limit value.
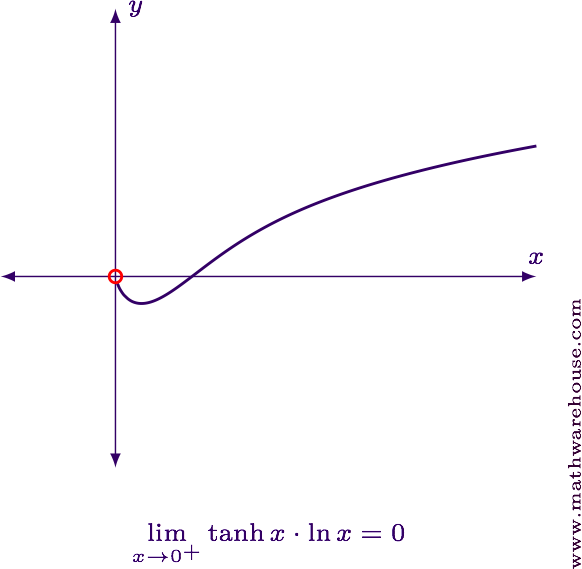
Evaluate the limit in its current form.
Since $$ y = \coth x $$ isn't as familiar as some other functions, here's its graph near $$ x = 0 $$. I'll also include the graph of $$ y = \sin x $$ since that will prove useful.
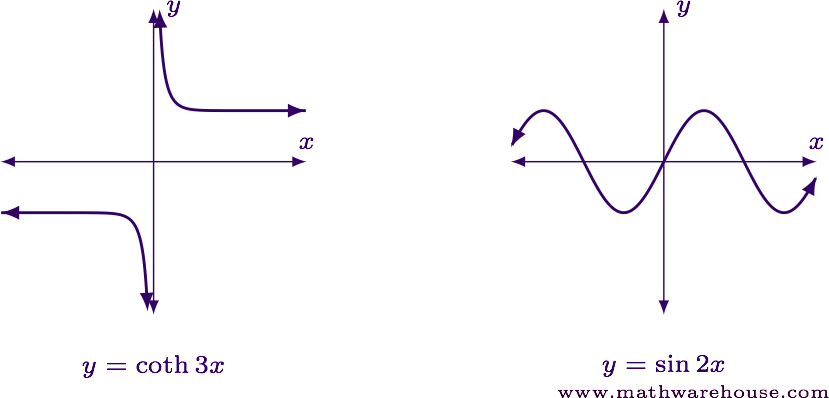
Since $$ \lim\limits_{x\to 0} \coth x = \pm \infty $$ depending on the direction in which $$ x $$ approaches zero, let's use one-sided limits to evaluate the limit for this question.
$$ \begin{align*}% \lim_{x\to 0^-} \blue{\sin 2x}\cdot \red{\coth 3x} & = \blue{\sin 0}\cdot \red{\coth 0} = \blue{-0}\cdot \red{(-\infty)} = 0\cdot \infty\\[6pt] \lim_{x\to 0^+} \blue{\sin 2x}\cdot \red{\coth 3x} & = \blue{\sin 0}\cdot \red{\coth 0} = \blue{+0}\cdot \red{(+\infty)} = 0\cdot \infty\\[6pt] \end{align*} $$
where "$$ -0 $$" means the function is approaching $$ 0 $$ from below, and "$$ +0 $$" means the function approaches $$ 0 $$ from above.
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Adjust the hyperbolic cotangent.
Thinking ahead: The derivative of $$ \sin 2x $$ is simple, and the reciprocal of $$ \coth 3x $$ is $$ \tanh 3x $$, the derivative of which just involves $$ \sech^2 $$.
-
Choice 2: Adjust the sine.
Thinking ahead: The derivative of $$ \coth 3x $$ is just involves a $$ \csch^2 $$, which isn't too bad. The reciprocal of the sine is a cosecant, the derivative of which is a product of cosecant and cotangent.
Between the two choices, the first one seems a little less messy, so let's try that one.
Rewrite the function and re-evaluate the limit.
$$ \displaystyle\lim_{x\to 0} \sin 2x\cdot \red{\coth 3x} = \displaystyle\lim_{x\to 0} \frac{\sin 2x}{\red{1/\coth 3x}} = \displaystyle\lim_{x\to 0} \frac{\sin 2x}{\red{\tanh 3x}} = \frac 0 0 $$
Apply L'Hôpital's rule, simplify and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 0} \frac{\sin 2x}{\tanh 3x} & = \lim_{x\to 0} \frac{\blue{\frac d {dx}\left(\sin 2x\right)}}{\red{\frac d {dx}\left(\tanh 3x\right)}}\\[6pt] & = \lim_{x\to 0} \frac{\blue{2\cos 2x}}{\red{3\sech^2 3x}}\\[6pt] & = \lim_{x\to 0} \frac 2 3\cos 2x\cdot \cosh^2 3x & \text{Simplifying}\\[6pt] & = \frac 2 3 (\cos 0)(\cosh^2 0)\\[6pt] & = \frac 2 3(1)(1)^2\\[6pt] & = \frac 2 3 \end{align*} $$
$$\displaystyle \lim_{x\to 0} \sin 2x\cdot \coth 3x = \frac 2 3$$
For reference, here is the graph of the function and the limit value.
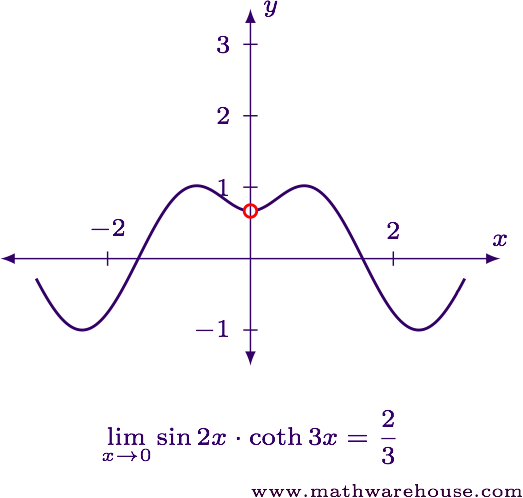
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to 0} \blue{x^2}\,\red{\sec^2\left(\frac{x - \pi} 2\right)} = \displaystyle\lim_{x\to 0} \blue 0 \cdot \red{\sec^2\left(-\frac \pi 2\right)} = \lim_{x\to 0} \blue 0 \cdot\red \infty $$
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Adjust the $$ \sec^2 $$.
Thinking ahead: The reciprocal of the $$ \sec^2 $$ is a $$ \cos^2 $$, the derivative of which involves a product of sine and cosine. The $$ x^2 $$ becomes just $$ 2x $$.
-
Choice 2: Adjust the $$ x^2 $$.
Thinking ahead: The derivative of the $$ \sec^2 $$ involves (because of the chain rule) the product of $$ \sec^2 $$ and $$ \tan $$, which is a little messy. The $$ x^{-2} $$, becomes $$ -2x^{-3} $$.
The trig derivatives are messy either way, but in Choice 1 the exponent on $$ x $$ is headed in the right direction. Let's try Choice 1.
Rewrite the function and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 0} x^2\,\red{\sec^2\left(\frac{x - \pi} 2\right)} & = \lim_{x\to 0} \frac{x^2}{\red{1/\sec^2\left(\frac{x - \pi} 2\right)}}\\[6pt] & = \lim_{x\to 0} \frac{x^2}{\red{\cos^2\left(\frac{x - \pi} 2\right)}}\\[6pt] & = \frac 0 {\cos^2\left(\frac{0 - \pi} 2\right)}\\[6pt] & = \frac 0 {\cos^2\left(-\frac \pi 2\right)}\\[6pt] & = \frac 0 0 \end{align*} $$
Apply L'Hôpital's rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 0} \frac{x^2} {% \cos^2\left(% \frac{x - \pi} 2 \right) } % & = \lim_{x\to 0} \frac{% \blue{% \frac d {dx}(x^2) } } {% \red{ \frac d {dx}\left(% \cos^2\left(% \frac 1 2 x - \frac \pi 2 \right) \right) } } \\[6pt] % & = \lim_{x\to 0} \frac{% \blue{2x} } {% \red{% 2\cos\left(% \frac 1 2 x - \frac \pi 2 \right) \left[% -\sin\left(% \frac 1 2 x - \frac \pi 2 \right) \right] \cdot \frac 1 2 } } \\[6pt] & = \lim_{x\to 0} -\frac{2x} {% \cos\left(% \frac 1 2 x - \frac \pi 2 \right) \sin\left(% \frac 1 2 x - \frac \pi 2 \right) } \\[6pt] & = -\frac 0 {% \cos\left(% - \frac \pi 2 \right) \sin\left(% - \frac \pi 2 \right) } \\[6pt] & = -\frac 0 {(0)(-1)}\\[6pt] & = \frac 0 0 \end{align*} $$
Simplify the limit before applying L'Hôpital's rule a second time
Before rushing into L'Hôpital's rule a second time (which would require a product rule in the denominator), notice it is the cosine that is going to $$ 0 $$ in the denominator. The sine isn't causing a problem. So, let's rewrite the limit as follows:
$$ \begin{align*} &\quad \lim_{x\to 0} -\frac{2x} {% \cos\left(% \frac 1 2 x - \frac \pi 2 \right) \sin\left(% \frac 1 2 x - \frac \pi 2 \right) } \\[6pt] % & = \lim_{x\to 0} \left(% -\frac{2x} {% \cos\left(% \frac 1 2 x - \frac \pi 2 \right) } \cdot \frac 1 { \sin\left(% \frac 1 2 x - \frac \pi 2 \right) } \right) \\[6pt] % & = \left(% \lim_{x\to 0} -\frac{2x} {% \cos\left(% \frac 1 2 x - \frac \pi 2 \right) } \right) \left( \lim_{\blue{x\to 0}} \frac 1 { \sin\left(% \frac 1 2 \blue x - \frac \pi 2 \right) } \right) \text{Properties of Limits} \\[6pt] % & = -\left(% \lim_{x\to 0} \frac{2x} {% \cos\left(% \frac 1 2 x - \frac \pi 2 \right) } \right) \left( \frac 1 { \sin\left(% \blue 0 - \frac \pi 2 \right) } \right) \\[6pt] % & = -\left(% \lim_{x\to 0} \frac{2x} {% \cos\left(% \frac 1 2 x - \frac \pi 2 \right) } \right)(-1) \\[6pt] % & = \lim_{x\to 0} \frac{2x} {% \cos\left(% \frac 1 2 x - \frac \pi 2 \right) } \end{align*} $$
Apply L'Hôpital's rule a second time and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 0} \frac{2x} {% \cos\left(% \frac 1 2 x - \frac \pi 2 \right) } & = \lim_{x\to 0} \frac{% \blue{% \frac d {dx} (2x) } } {% \red{% \frac d {dx} \left(% \cos\left(% \frac 1 2 x - \frac \pi 2 \right) \right) } } \\[6pt] & = \lim_{x\to 0} \frac{% \blue 2 } {% \red{% -\sin\left(% \frac 1 2 x - \frac \pi 2 \right) \cdot \frac 1 2 } } \\[6pt] & = \lim_{x\to 0} \frac 4 {% -\sin\left(% \frac 1 2 x - \frac \pi 2 \right) } \\[6pt] & = \frac 4 {% -\sin\left(% - \frac \pi 2 \right) } \\[6pt] & = \frac 4 {-(-1)} \\[6pt] & = 4 \end{align*} $$
$$ \displaystyle \lim_{x\to 0} x^2\sec^2\left(\frac{x - \pi} 2\right) = 4 $$
For reference, here is the graph of the function along with the limit value.
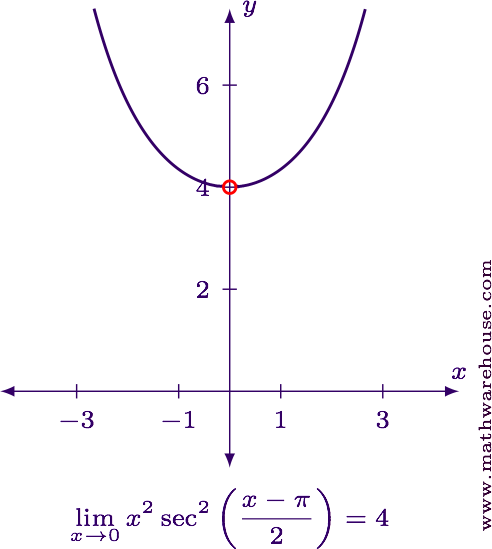
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to 2^-} \blue{% \frac x {x-2} } \,\red{% \cos\left(% \frac \pi 4 x \right) } = \blue{ \frac 2 0 } \cdot \red{% \cos\left(% \frac \pi 2 \right) } = \blue \infty \cdot \red 0 $$
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Adjust the cosine.
Thinking ahead: The reciprocal of the cosine is a secant, the derivative of which is a $$ \sec()\cdot \tan() $$. The algebraic factor will require the quotient rule to differentiate.
-
Choice 2: Adjust the algebraic factor.
Thinking ahead: The derivative of the cosine is just a negative sine. The reciprocal of the algebraic factor simplifies down to $$ 1 - 2x^{-1} $$, which is easy to differentiate.
Choice 2 clearly seems more straightforward. Let's start there.
Rewrite the function and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 2^-} \blue{% \frac x {x-2} }\, \cos\left(% \frac \pi 4 x \right) % & = \lim_{x\to 2^-} \frac{% \cos\left(% \frac \pi 4 x \right) } {% \blue{% \frac {x-2} x } } && \text{Adjust} \\[6pt] % & = \lim_{x\to 2^-} \frac{ \cos\left(% \frac \pi 4 x \right) } {% \blue{1 - \frac 2 x} } && \text{Simplify} \\[6pt] % & = \frac{% \cos\left(% \frac \pi 2 \right)} { \blue{1 - \frac 2 2} } && \text{Re-evaluate the Limit} \\[6pt] % & = \frac 0 0 \end{align*} $$
Apply L'Hôpital's rule, simplify and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 2^-} \frac{% \cos\left(% \frac \pi 4 x \right) } {% 1 - \frac 2 x } % & = \lim_{x\to 2^-} \frac{% \red{% \frac d {dx}\left(% \cos \frac \pi 4 x \right) } } {% \blue{% \frac d {dx}\left(% 1 - 2x^{-1} \right) } } \\[6pt] % & = \lim_{x\to 2^-} \frac{% \red{% -\frac \pi 4 \sin\left(% \frac \pi 4 x \right) } } {% \blue{% 2x^{-2} } } \\[6pt] % & = \lim_{x\to 2^-} -\frac \pi 8 \cdot \frac{% \sin\left(% \frac \pi 4 x \right) }{% x^{-2} } && \text{Simplifying} \\[6pt] % & = \lim_{x\to 2^-} -\frac \pi 8 x^2\sin\left(% \frac \pi 4 x \right) \\[6pt] % & = -\frac \pi 8 \cdot 4\sin\left(% \frac \pi 2 \right) && \text{Re-evaluating} \\[6pt] % & = -\frac \pi 2 (1) \\[6pt] & = -\frac \pi 2 \end{align*} $$
$$ \displaystyle \lim_{x\to 2^-} \frac x {x-2}\cos\left(\frac \pi 4 x\right) = -\frac \pi 2 $$
For reference, here is the graph of the function and the limit value.
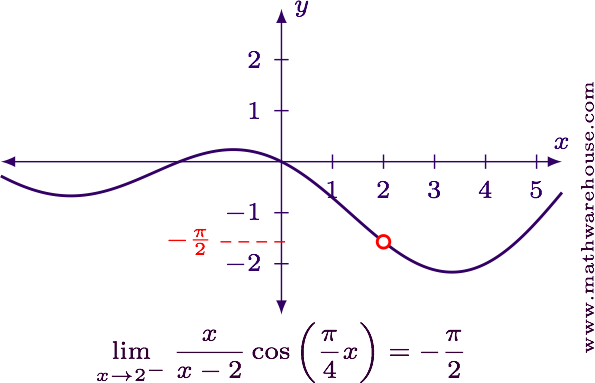
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to 1^+} \blue{% \sqrt{% x^2-1 } } \cdot\red{% \cot\left(% \pi x \right) } = \blue{% \sqrt 0 } \cdot\red{ \cot \pi } = 0 \cdot \infty $$
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Adjust the cotangent.
Thinking ahead: The derivative of the square root involves a $$(x^2-1)^{-1/2}$$. The reciprocal of the cotangent is a tangent, the derivative of which is a $$ \sec^2() $$.
-
Choice 2: Adjust the square-root.
Thinking ahead: The derivative of the cotangent is a negative $$ \csc^2() $$. The reciprocal of the square root will be $$(x^2-1)^{-1/2}$$. Its derivative will involve $$(x^2-1)^{-3/2}$$
Neither choice looks 'nicer', but the square root ends up with a smaller exponent in Choice 1.
Rewrite the function and re-evaluate the limit.
$$ \displaystyle\lim_{x\to 1^+} \sqrt{x^2-1} \cdot\red{% \cot\left(% \pi x \right) } = \displaystyle\lim_{x\to 1^+} \frac{% \sqrt{x^2-1} } {% \red{% 1/\cot\left(% \pi x \right) } } = \displaystyle\lim_{x\to 1^+} \frac{% \sqrt{x^2-1} } {% \red{% \tan\left(% \pi x \right) } } = \frac 0 0 $$
Use L'Hôpital's rule, simplify and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 1^+} \frac{% \sqrt{x^2-1} } {% \red{% \tan\left(% \pi x \right) } } % & = \lim_{x\to 1^+} \frac{ \blue{% \frac d {dx}(% x^2-1 )^{1/2} } } {% \red{% \frac d {dx}\left(% \tan \pi x \right) } } \\[6pt] % & = \lim_{x\to 1^+} \frac{% \blue{% \frac 1 2 (x^2-1)^{-1/2} (2x) } } {% \red{% \frac \pi 4 \sec^2 \pi x } } \\[6pt] % & = \lim_{x\to 1^+} \frac{% \blue{% \frac 1 2 (x^2-1)^{-1/2} (2x) } } 1 \cdot \frac 1 {% \red{% \frac \pi 4 \sec^2 (\pi x) } } && \text{Simplifying} \\[6pt] % & = \lim_{x\to 1^+} \frac{% \blue{2x} } {% \blue{% 2(x^2-1)^{1/2} } } \cdot\frac{% \red{% \cos^2 \pi x } } {% \red{\pi/4} } \\[6pt] % & = \lim_{x\to 1^+} \frac x {% \sqrt{x^2-1} } \cdot\frac 4 \pi \cos^2 \pi x \\[6pt] % & = \frac 1 {% \sqrt{1-1} } \cdot \frac 4 \pi \cos^2 \pi && \text{Re-evaluating the Limit} \\[6pt] % & = \frac 1 0 \cdot \frac 4 \pi \\[6pt] % & = \infty \end{align*} $$
$$ \displaystyle% \lim_{x\to 1^+} \sqrt{x^2-1} \cot\left(% \pi x \right) = \infty $$
For reference, here is the graph of the function near $$ x = 1 $$.
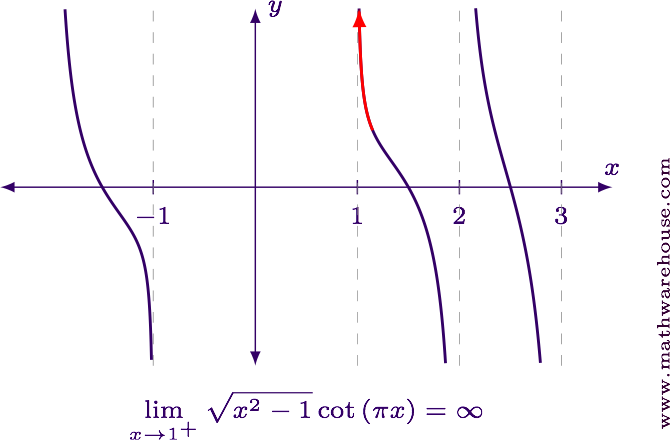
Evaluate the limit in its current form.
For many, the hyperbolic cotangent isn't a familiar function. So let's examine its graph.
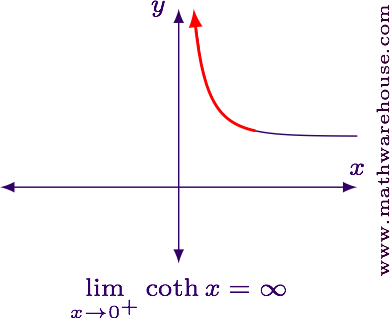
With this in mind, evaluating our limit in its current form gives us
$$ \displaystyle\lim_{x\to 0^+} \blue{% \sqrt{2x} } \cdot\red{% \coth\left(% \sqrt x \right) } = \displaystyle\lim_{x\to 0^+} \blue{\sqrt 0} \cdot\red{% \coth 0 } = \blue 0 \cdot \red \infty $$
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Adjust the hyperbolic cotangent.
Thinking ahead: The derivative of the square root will have an exponent of $$ -1/2 $$. The reciprocal of the $$ \coth() $$ is just $$ \tanh() $$, the derivative of which is a $$ \sech^2() $$.
-
Choice 2: Adjust the square-root.
Thinking ahead: The derivative of the hyperbolic cotangent is a $$ \csch^2() $$. The $$ (2x)^{-1/2} $$ has a derivative with an exponent of $$ -3/2 $$.
Neither choice seems better or worse really, but after the derivatives the first choice has a nicer exponent on the square root. Let's try that.
Rewrite the function and re-evaluate the limit.
$$ \displaystyle\lim_{x\to 0^+} \sqrt{2x} \cdot\red{% \coth\left(% \sqrt x \right) } % = \displaystyle\lim_{x\to 0^+} \frac{% \sqrt{2x} } {% \red{% 1 / \coth\left(% \sqrt x \right) } } % = \displaystyle\lim_{x\to 0^+} \frac{% \sqrt{2x} } {% \red{% \tanh\left(% \sqrt x \right) } } % = \frac 0 0 $$
Apply L'Hôpital's rule, simplify and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 0^+} \frac{% \sqrt{2x} } {% \tanh\left(% \sqrt x \right) } % & = \lim_{x\to 0^+} \frac{% \blue{% \frac d {dx} (2x)^{1/2} } } {% \red{% \frac d {dx} \tanh\left(% x^{1/2} \right) } } \\[6pt] % & = \lim_{x\to 0^+} \frac{% \blue{% \frac 1 2 (2x)^{-1/2} \cdot 2 } } {% \red{% \sech^2\left(% x^{1/2} \right) \cdot \frac 1 2 x^{-1/2} } } \\[6pt] % & = \lim_{x\to 0^+} \frac{% 2\cdot (2x)^{-1/2} } {% \sech^2\left(% x^{1/2} \right) \cdot x^{-1/2} } && \text{Simplifying} \\[6pt] % & = \lim_{x\to 0^+} \frac{% 2\cdot 2^{-1/2} \cdot \cancelred{% x^{-1/2} } } {% \sech^2\left(% x^{1/2} \right) \cdot \cancelred{% x^{-1/2} } } \\[6pt] % & = \frac{% 2^{1/2} } {% \sech^2 0 } \\[6pt] % & = \sqrt 2 \end{align*} $$
$$ \displaystyle \lim_{x\to 0^+} \sqrt{2x} \cdot\coth\left(% \sqrt x \right) = \sqrt 2 $$
For reference, here is the graph of the function near $$ x = 0 $$.
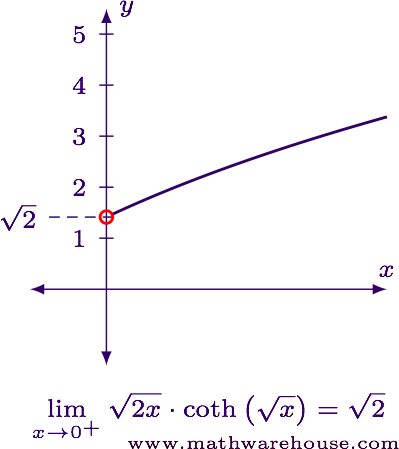
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to 0} \blue{% \cot x } \cdot\red{% \arcsin x } = \blue{% \cot 0 } \cdot\red{% \arcsin 0 } = \blue 0 \cdot \red \infty $$
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Adjust the arcsine.
Thinking ahead: The derivative of the cotangent is just easy, but differentiating $$(\arcsin x)^{-1}$$ will be ugly
-
Choice 2: Adjust the cotangent.
Thinking ahead: The derivative of the arcsine is easy, and the reciprocal of the cotangent is just a tangent.
Choice 2 seems the obvious one to try first.
Rewrite the function and re-evaluate the limit.
$$ \displaystyle\lim_{x\to 0} \blue{\cot x} \cdot \arcsin x = \displaystyle\lim_{x\to 0} \frac{% \arcsin x } {% \blue{% 1/\cot x } } = \displaystyle\lim_{x\to 0} \frac{% \arcsin x } {% \blue{% \tan x } } = \frac 0 0 $$
Use L'Hôpital's rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 0} \frac{% \arcsin x } {% \tan x } % & = \lim_{x\to 0} \frac{% \red{% \frac d {dx}\left(% \arcsin x \right) } } {% \blue{% \frac d {dx}\left(% \tan x \right) } } \\[6pt] % & = \lim_{x\to 0} \frac{% \red{% \frac 1 {% \sqrt{1 - x^2} } } } {% \blue{% \sec^2 x } } \\[6pt] % & = \lim_{x\to 0} \frac{% \cos^2 x } {% \sqrt{1 - x^2} } \\[6pt] % & = \frac{% \cos^2 0 } {% \sqrt 1 } \\[6pt] % & = 1 \end{align*} $$
$$ \displaystyle \lim_{x\to 0} \cot x \cdot \arcsin x = 1 $$
For reference, here is the graph of the function along with the limit value.
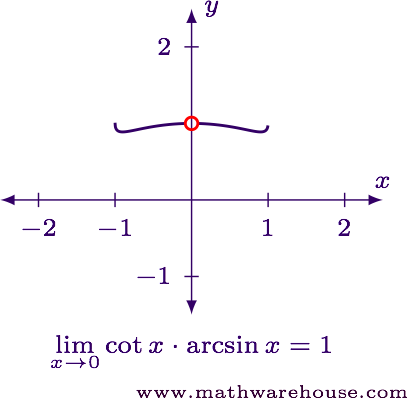
Evaluate the limit in its current form.
$$ \displaystyle\lim_{x\to 1^+} \csc(\pi x)\arcsec^2 x = \displaystyle\lim_{x\to 1^+} \blue{\csc(\pi x)}\red{(\arcsec x)^2} = \blue{\csc(\pi)}\red{(\arcsec 1)^2} = \blue{-\infty}\cdot \red 0 $$
Determine which form ($$ \frac 0 0 $$ or $$ \frac \infty \infty $$) to use.
-
Choice 1: Adjust the arcsecant.
Thinking ahead: The derivative of cosecant is just easy, but $$ (\arcsec x)^{-2} $$ will have a rather messy derivative.
-
Choice 2: Adjust the cosecant.
Thinking ahead: The derivative of $$ (\arcsec x)^2 $$ isn't really going to be better (or worse) than in the previous choice, while the reciprocal of the cosecant is just a sine.
Neither choice seems to be easier, but let's pick Choice 2 since the derivative of a sine is a little simpler than that of a cosecant.
Rewrite the function and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 1^+} \blue{\csc(\pi x)}\,(\arcsec x)^2 & = \lim_{x\to 1^+} \frac{(\arcsec x)^2}{\blue{1/\csc \pi x}}\\[6pt] & = \lim_{x\to 1^+} \frac{(\arcsec x)^2}{\blue{\sin \pi x}}\\[6pt] & = \frac{(\arcsec 1)^2}{\blue{\sin \pi}}\\[6pt] & = \frac{0}{\blue 0} \end{align*} $$
Apply L'Hôpital's rule and re-evaluate the limit.
$$ \begin{align*} \lim_{x\to 1^+} \frac{(\arcsec x)^2}{\sin \pi x} & = \lim_{x\to 1^+} \frac{\red{\frac d {dx}\left[(\arcsec x)^2\right]}}{\blue{\frac d {dx} \left(\sin \pi x \right)}}\\[6pt] & = \lim_{x\to 1^+} \frac{\red{2(\arcsec x)\cdot \frac 1 {|x|\sqrt{x^2 - 1}}}}{\blue{\pi\cos \pi x}}\\[6pt] & = \lim_{x\to 1^+} \frac{2\arcsec x}{\pi|x|\cos(\pi x)\sqrt{x^2 - 1}} & \text{Simplified}\\[6pt] & = \frac{2\arcsec 1}{\pi\cos(\pi)\sqrt{1 - 1}}\\[6pt] & = \frac{2(0)}{\pi(-1)(0)}\\[6pt] & = \frac 0 0 \end{align*} $$
Should we try L'Hôpital's rule again, or switch to the $$ \frac \infty \infty $$ form?
Notice that the power on the arcsecant has been reduced. So this seems to be a good indication that we are on the right track.
Apply L'Hôpital's rule again, and re-evaluate the limit.
Before we just jump directly into the next application of L'Hôpital's rule, let's make sure we're not making things more complicated than they need to be. Notice that
$$ \displaystyle\lim_{x\to 1^+} \frac{2\arcsec x}{\pi|x|\cos(\pi x)\sqrt{x^2 - 1}} = \frac{\red{2}\,\blue{\arcsec 1}}{\red{\pi|1|\cos \pi}\blue{\sqrt{1^2 - 1}}} = \red{\frac 2 {\pi|1|\cos \pi}}\cdot \blue{\frac{\arcsec 1}{\sqrt{1^2 - 1}}} = \red{-\frac 2 \pi}\cdot \blue{\frac 0 0} $$
Only the parts in blue actually cause the $$ \frac 0 0 $$ form at this stage. So we only need L'Hôpital's rule for those parts.
$$ \begin{align*} \lim_{x\to 1^+} \frac{2\arcsec x}{\pi|x|\cos(\pi x)\sqrt{x^2 - 1}} & = \left(% \lim_{x\to 1^+} \frac 2 {% \pi|x|\cos(\pi x) } \right) \left(% \lim_{x\to 1^+} \frac{% \arcsec x } {% \sqrt{x^2 - 1} } \right) \\[6pt] % & = \left(% -\frac 2 \pi \right) \cdot \left(% \lim_{x\to 1^+} \frac{% \arcsec x } {% \sqrt{x^2 - 1} } \right) \\[6pt] % & = -\frac 2 \pi \cdot \lim_{x\to 1^+} \frac{\blue{\frac d {dx}\left(\arcsec x\right)}}{\red{\frac d {dx}\left[\left(x^2 - 1\right)^{1/2}\right]}}\\[6pt] & = -\frac 2 \pi \cdot \lim_{x\to 1^+} \frac{\blue{\frac 1 {|x|\sqrt{x^2 - 1}}}}{\red{\frac 1 2\left(x^2 - 1\right)^{-1/2}\cdot 2x}}\\[6pt] & = -\frac 2 \pi \cdot \lim_{x\to 1^+} \blue{\frac 1 {|x|\sqrt{x^2 - 1}}} \cdot\red{\frac{\sqrt{x^2 - 1}} x}&\text{Simplifying}\\[6pt] & = -\frac 2 \pi \cdot \lim_{x\to 1^+} \frac 1 {|x|\cancelred{\sqrt{x^2 - 1}}} \cdot \frac{\cancelred{\sqrt{x^2 - 1}}} x\\[6pt] & = -\frac 2 \pi \cdot \lim_{x\to 1^+} \frac 1 {x^2}\\[6pt] & = -\frac 2 \pi \cdot (1)\\[6pt] & = -\frac 2 \pi \end{align*} $$
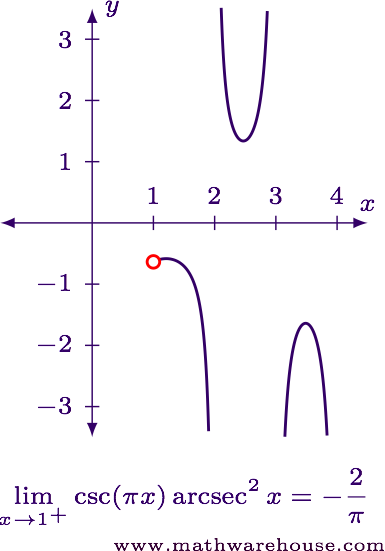
$$ \displaystyle \lim_{x\to 1^+} \csc(\pi x)\arcsec^2 x = -\frac 2 \pi $$
For reference, here is the graph of the function and the limit value.