How to Use the Chain Rule for Derivatives

Example 1

Suppose $$\displaystyle h(x) = \sin(x^2)$$. Find $$h'(x)$$.

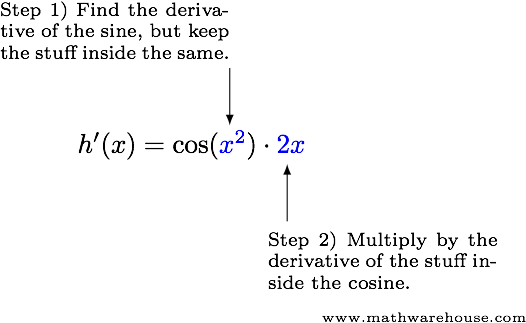Answer

$$h'(x) = 2x\cos(x^2)$$

Example 2

Suppose $$\displaystyle f(x) = \sqrt{x^3+2}$$. Find $$f'(x)$$.

Step 1

Write the square-root in exponent form.

$$ f(x) = (x^3+2)^{1/2} $$

Step 2

Use the power rule and the chain rule.

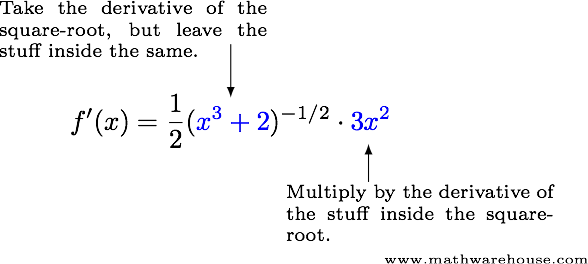Step 3

Simplify $$f'$$.

$$ f'(x) = \frac 3 2 x^2 (x^3 + 2)^{-1/2} $$

Step 4

(Optional) Write the derivative in radical form.

$$ \begin{align*} f'(x) & = \frac 3 2 x^2 (x^3 + 2)^{-1/2}\\[6pt] & = \frac 3 2 x^2 \cdot \frac 1 {x^3 + 2)^{1/2}}\\[6pt] & = \frac 3 2 x^2 \cdot \frac 1 {\sqrt{x^3 + 2}}\\[6pt] & = \frac{3x^2}{2\sqrt{x^3+2}} \end{align*} $$

Answer

$$\displaystyle f'(x) = \frac{3x^2}{2\sqrt{x^3+2}}$$.

Example 3

Use the chain rule to find $$\displaystyle \frac d {dx}\left(\sec x\right)$$.

Step 1

Rewrite the function in terms of the cosine.

$$ \sec x = \frac 1 {\cos x} = \big(\cos x\big)^{-1} $$

Step 2

Differentiate using the chain rule.

$$ \begin{align*} \frac d {dx}\left(\sec x\right) & = \frac d {dx}\left[(\cos x)^{-1}\right]\\[6pt] & = -1(\cos x)^{-2}\cdot (-\sin x)\\[6pt] & = -\frac 1 {\cos^2 x} \cdot (-\sin x)\\[6pt] & = \frac{\sin x}{\cos^2 x} \end{align*} $$

Step 3

Simplify by separating into two fractions and using trigonometric identities.

$$ \begin{align*} \frac d {dx}\left(\sec x\right) & = \frac{\sin x}{\cos^2 x}\\[6pt] & = \frac 1 {\cos x} \cdot \frac{\sin x}{\cos x}\\[6pt] & = \sec x \tan x \end{align*} $$

Answer

$$\displaystyle \frac d {dx}\left(\sec x\right) = \sec x \tan x$$

Example 4

Suppose $$f(x) = e^{-x^2}\sin(x^3)$$. Find $$f'(x)$$.

Notice that this function will require both the product rule and the chain rule.

Step 1

Identify the factors in the function.

$$ f(x) = \blue{e^{-x^2}}\red{\sin(x^3)} $$

Step 2

Differentiate using the product rule.

Step 3

(Optional) Factor the derivative.

$$ \begin{align*} f'(x) & = -2x\blue{e^{-x^2}}\sin(x^3) + \blue{e^{-x^2}}\,3x^2\cos(x^3)\\[6pt] & = \blue{e^{-x^2}}\left(-2\red x\sin(x^3) + 3\red{x^2}\cos(x^3)\right)\\[6pt] & = \red xe^{-x^2}\left(-2\sin(x^3) + 3x\cos(x^3)\right)\\[6pt] & = xe^{-x^2}\left(3x\cos(x^3)-2\sin(x^3)\right) \end{align*} $$

Answer

$$\displaystyle f'(x) = xe^{-x^2}\left(3x\cos(x^3)-2\sin(x^3)\right)$$.

Example 5

Suppose $$f(x) = \sqrt{\cos(5x+1)}$$. Find $$f'(x)$$.

Notice that $$f$$ is a composition of three functions. This means we will need to use the chain rule twice.

Step 1

Write the square-root as an exponent.

$$ f(x) = [\cos(5x+1)]^{1/2} $$

Step 2

Use the power rule and the chain rule for the square-root.

$$ f'(x) = \frac 1 2[\blue{\cos(5x + 1)}]^{-1/2}\cdot \frac d {dx}\left(\blue{\cos(5x+1)}\right) $$

Step 3

Find the derivative of the cosine.

$$ f'(x) = \frac 1 2[\cos(5x + 1)]^{-1/2}\cdot \left(-\sin(\red{5x+1)}\right)\cdot \frac d {dx}(\red{5x+1}) $$

Step 4

Find the derivative of the linear function.

$$ f'(x) = \frac 1 2[\cos(5x + 1)]^{-1/2}\cdot \left(-\sin(5x+1)\right)\cdot 5 $$

Step 5

Simplify the derivative.

$$ \begin{align*}% f'(x) & = \frac 1 2[\cos(5x + 1)]^{-1/2}\cdot \left(-\sin(5x+1)\right)\cdot 5\\[6pt] & = -\frac 5 2[\cos(5x + 1)]^{-1/2}\cdot \left(\sin(5x+1)\right)\\[6pt] & = -\frac 5 2\cdot \frac 1 {[\cos(5x + 1)]^{1/2}}\cdot \left(\sin(5x+1)\right)\\[6pt] &= -\frac{5\sin(5x+1)}{2\sqrt{\cos(5x+1)}} \end{align*} $$

Answer

$$\displaystyle -\frac{5\sin(5x+1)}{2\sqrt{\cos(5x+1)}}$$.