Example 1

Try to use L'Hôpital's Rule to evaluate $$\displaystyle \lim_{x\to3} \frac{2x + 7}{4x+1}$$

Attempted Solution

Step 1

Apply L'Hôpital's rule to the limit and then evaluate.

$$ \begin{align*} \lim_{x\to 3}\frac{2x + 7}{4x+1} & = \lim_{x\to 3}\frac{\blue{\frac d {dx}(2x + 7)}}{\red{\frac d {dx}(4x+1)}} = \lim_{x\to 3}\frac{\blue 2}{\red 4} = \frac 1 2 \end{align*} $$

However, this is incorrect! An inspection of the graph of the function near $$x=3$$ we see:

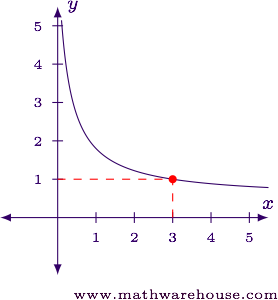
The actual limit value should be near $$1$$. Why didn't L'Hôpital's rule work?

What went wrong ?

Remember, L'Hôpital's rule works ONLY with indeterminate limits with the form $$\frac 0 0$$ OR $$\frac \infty \infty$$.

This is why in each example and solution in the previous lesson (What is L'Hôpital's Rule?) the first step was always to evaluate the limit in its current form to make sure it was indeterminate, and specifically has the form $$\frac 0 0$$ or $$\frac \infty \infty$$.

Let's work out the correct solution.

Correct Solution

Step 1

Evaluate the limit in its current form to see if L'Hôpital's Rule is needed.

$$ \displaystyle\lim_{\blue{x\to3}} \frac{2x + 7}{4x+1} = \frac{2\blue{(3)}+7}{4\blue{(3)}+1} = \frac{13}{13} = 1 $$

We can see that this limit is not indeterminate, so it doesn't require L'Hôpital's Rule.

Answer

$$ \displaystyle \lim_{x\to3} \frac{2x + 7}{4x+1} = 1 $$

Example 2

Try to use L'Hôpital's Rule to evaluate $$\displaystyle \lim_{x\to0^+} \ln x\cdot \sin x$$.

Attempted Solution

As in the previous example, this one is intended to show you a problem with applying L'Hôpital's Rule incorrectly.

Step 1

Show that this limit is indeterminate by evaluating it in its current form.

$$ \displaystyle\lim_{x\to0^+} \blue{\ln x}\cdot \red{\sin x} = \blue{-\infty}\cdot \red 0 $$

This is an indeterminate value since one factor becomes larger while the other becomes smaller. Without more information we can't determine what actually happens in the limit.

Step 2

Take the derivative of each part and re-evaluate the limit. (Note: this is where the error occurs in our solution. Do you see what the problem is?)

$$ \begin{align*} \lim_{x\to0^+} \ln x\cdot \sin x & = \lim_{x\to0^+} \blue{\frac d {dx}\left(\ln x\right)}\cdot \red{\frac d {dx}\left(\sin x\right)}\\[6pt] & = \lim_{x\to0^+} \blue{\frac 1 x}\cdot \red{\cos x}\\[6pt] & = \lim_{x\to0^+} \frac{\cos x} x\\[6pt] & = \frac{\cos 0} 0\\[6pt] & = \frac 1 0\\[6pt] & = \infty \end{align*} $$

However, this is incorrect as the graph of the function near $$x = 0$$ shows.

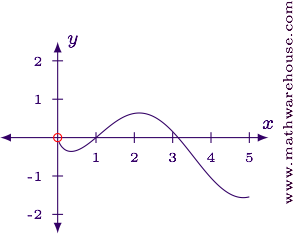
What Went Wrong

It isn't enough for a limit to simply be indeterminate. In order to use L'Hôopital's Rule, the limit must have the form $$\frac 0 0$$ or $$\frac \infty \infty$$.

Correct Solution

For indeterminate limits that have a $$0\cdot \infty$$ form, we can make some algebraic adjustments so the limit changes to a $$\frac 0 0$$ or $$\frac \infty \infty$$ form, and thus utilize L'Hôpital's rule correctly. This type of limit is discussed in detail in the next lesson: L'Hôpital's Rule and $$0\cdot\infty$$ Forms

Example 3

Use L'Hôpital's rule to evaluate $$\displaystyle \lim_{x\to0^+} \frac{\ln x}{1/x}$$.

Note that this particular example is not one of the forms from an earlier lesson. So, without L'Hôpital's Rule, we would be hard pressed to evaluate it.

Attempted Solution

Step 1

Evaluate the limit in its current form.

$$ \displaystyle\lim_{x\to0^+} \frac{\ln x}{1/x} = \frac{-\infty} \infty $$

Step 2

Apply L'Hôpital's rule repeatedly, evaluating the limit each time.

$$ \begin{align*} \lim_{x\to0^+} \frac{\ln x}{1/x} & = \lim_{x\to0^+} \frac{\blue{\frac d {dx}\left(\ln x\right)}}{\red{\frac d {dx}\left(1/x\right)}} && \mbox{L'Hôpital's rule 1st Time}\\[6pt] & = \lim_{x\to0^+} \frac{1/x}{-1/x^2} = \frac \infty {-\infty}\\[6pt] & = \lim_{x\to0^+} \frac{\blue{\frac d {dx}\left(1/x\right)}}{\red{\frac d {dx}\left(-1/x^2\right)}} && \mbox{L'Hôpital's rule 2nd Time}\\[6pt] & = \lim_{x\to0^+} \frac{-1/x^2}{2/x^3} = \frac {-\infty} \infty\\[6pt] & = \lim_{x\to0^+} \frac{\blue{\frac d {dx}\left(-1/x^2\right)}}{\red{\frac d {dx}\left(2/x^3\right)}} && \mbox{L'Hôpital's rule 3rd Time}\\[6pt] & = \lim_{x\to0^+} \frac{2/x^3}{-6/x^4} = \frac \infty {-\infty} \end{align*} $$

Let's look more closely at the string of limits we calculated above.

$$ \displaystyle\lim_{x\to0^+} \frac{\ln x}{1/x} = \lim_{x\to0^+} \frac{1/x}{-1/x^2} = \lim_{x\to0^+} \frac{-1/x^2}{2/x^3} = \lim_{x\to0^+} \frac{2/x^3}{-6/x^4} = \frac \infty \infty $$

What's Going Wrong

Each time we apply L'Hôpital's rule, we see the powers of $$x$$ increase, but the overall form of the limit doesn't change.

Instead of blundering forward with repeated applications of the rule, it is important (even critical) that we simplify the function at each stage.

Correct Solution

Step 1

Verify the form: $$\displaystyle \lim_{x\to0^+} \frac{\ln x}{1/x} = \frac{-\infty} \infty$$

Step 2

Apply L'Hôpital's rule once.

$$ \begin{align*} \lim_{x\to0^+} \frac{\ln x}{1/x} & = \lim_{x\to0^+} \frac{\blue{\frac d {dx}\left(\ln x\right)}}{\red{\frac d {dx}\left(1/x\right)}} = \lim_{x\to0^+} \frac{1/x}{-1/x^2} \end{align*} $$

Step 3

Simplify the result, then re-evaluate the limit.

$$ \begin{align*} \lim_{x\to0^+} \frac{1/x}{-1/x^2} & = \lim_{x\to0^+} \frac 1 x\cdot \left(\frac{x^2}{-1}\right) = \lim_{x\to0^+} -\frac{x^2} x = \lim_{x\to0^+} -x = 0 \end{align*} $$

As my venerated Calculus I professor told me many years ago, "Simplifying is (almost) always a good idea!"

Answer

$$\displaystyle \lim_{x\to0^+} \frac{\ln x}{1/x} = 0$$

For reference, here is the graph of the function and the limit value.

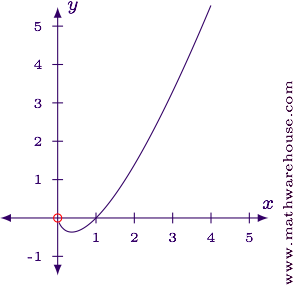
Unfortunately, even when we are careful about the form and our approach, L'Hôpital's rule doesn't always yield an answer, as shown in the next example.

Example 4

Try using L'Hôpital's rule to evaluate $$\displaystyle \lim_{x\to\infty} \frac{\sqrt{4x^2+3}}{x+3}$$.

Attempted Solution

Step 1

Evaluate the limit in its current form.

$$ \displaystyle\lim_{x\to\infty} \frac{\sqrt{4x^2+3}}{x+3} = \frac \infty \infty $$

Notice that this limit is both indeterminate AND has the correct form for L'Hôpital's Rule.

Step 2

Apply L'Hôpital's rule to the limit, and then re-evaluate the limit.

$$ \begin{align*} \lim_{x\to\infty} \frac{\sqrt{4x^2+3}}{x+3} & = \lim_{x\to\infty} \frac{(4x^2+3)^{1/2}}{x+3} &&\mbox{Rewriting the original limit}\\[6pt] & = \lim_{x\to\infty} \frac{\blue{\frac d {dx}(4x^2+3)^{1/2}}}{\red{\frac d {dx}(x+3)}} && \mbox{L'Hôpital's rule}\\[6pt] & = \lim_{x\to\infty} \frac{\frac 1 2(4x^2+3)^{-1/2}\cdot 8x}{1}\\[6pt] & = \lim_{x\to\infty} \frac{4x}{(4x^2+3)^{1/2}} &&\mbox{Simplifying}\\[6pt] & = \frac \infty \infty \end{align*} $$

Step 3

Apply L'Hôpital's rule a second time, and re-evaluate the limit.

$$ \begin{align*} \lim_{x\to\infty} \frac{4x}{(4x^2+3)^{1/2}} & = \lim_{x\to\infty} \frac{\blue{\frac d {dx}(4x)}}{\red{\frac d {dx}(4x^2+3)^{1/2}}} && \mbox{L'Hôpital's rule}\\[6pt] & = \lim_{x\to\infty} \frac{4}{\frac 1 2(4x^2+3)^{-1/2}\cdot 8x}\\[6pt] & = \lim_{x\to\infty} \frac{(4x^2+3)^{1/2}}{x} && \mbox{Simplify}\\[6pt] & = \frac \infty \infty \end{align*} $$

Notice that this is essentially the same type of function we started out with:

$$f(x) = \frac{\sqrt{\mbox{Quadratic}}}{\mbox{Linear}}.$$

Another application of L'Hôpital's Rule is likely to just start taking us around in circles. Let's try it, just to be sure.

Step 4

Try L'Hôpital's Rule again.

$$ \begin{align*} \lim_{x\to\infty} \frac{(4x^2+3)^{1/2}}{x} & = \lim_{x\to\infty} \frac{\blue{\frac d {dx}(4x^2+3)^{1/2}}}{\red{\frac d {dx}(x)}} = \lim_{x\to\infty} \frac{\frac 1 2(4x^2+3)^{-1/2}\cdot 8x}{1} = \lim_{x\to\infty} \frac{4x}{(4x^2+3)^{1/2}} \end{align*} $$

This is exactly the function we got at the end of Step 2! No matter how many times we try using L'Hôpital's rule, it will never yield a limit value. The process will just keep cycling around and around.

What's Going Wrong

L'Hôpital's rule isn't failing here. All the rule guarantees is

$$ \underbrace{\displaystyle\lim_{x\to a} \frac{f(x)}{g(x)} = \displaystyle\lim_{x\to a} \frac{df/dx}{dg/dx}}_{\mbox{if the limits exist, the limits are equal.}} $$

L'Hôspital's Rule does not guarantee the second limit can be evaluated.

Now, as we've seen, most of the time the second (or third, or fourth, or ...) limits we get from the rule have a simpler form and the new limit is more easily evaluated. But as this example shows, that isn't always the case.

Correct Solution

To evaluate this limit, we use a technique we discussed in an earlier lesson.

Step 1

Factor the $$x^2$$ out of the square-root.

$$ \begin{align*}% \lim_{x\to\infty} \frac{\sqrt{4x^2+3}}{x+3} & = \lim_{x\to\infty} \frac{\sqrt{x^2\left(4+\frac 3 {x^2}\right)}}{x+3}= \lim_{x\to\infty} \frac{\sqrt{x^2}\cdot\sqrt{4+\frac 3 {x^2}}}{x+3} = \lim_{x\to\infty} \frac{|x|\cdot\sqrt{4+\frac 3 {x^2}}}{x+3} \end{align*} $$

Step 2

Based on the limit, determine if $$|x|$$ should be replaced with $$x$$ or $$-x$$.

Since the limit examines positive values of $$x$$, we replace $$|x|$$ with just $$x$$.

$$ \displaystyle\lim_{x\to\infty} \frac{x\cdot\sqrt{4+\frac 3 {x^2}}}{x+3} $$

Step 3

Factor the $$x$$ out of the denominator, then simplify.

$$ \displaystyle\lim_{x\to\infty} \frac{x\cdot\sqrt{4+\frac 3 {x^2}}}{x+3} = \lim_{x\to\infty} \frac{x\cdot\sqrt{4+\frac 3 {x^2}}}{x\left(1+\frac 3 x\right)} = \lim_{x\to\infty} \frac{\sqrt{4+\frac 3 {x^2}}}{1+\frac 3 x} $$

Step 4

Evaluate the limit.

Answer

$$\displaystyle \lim_{x\to\infty} \frac{\sqrt{4x^2+3}}{x+3} = 2$$

For reference, here is the graph of the function.

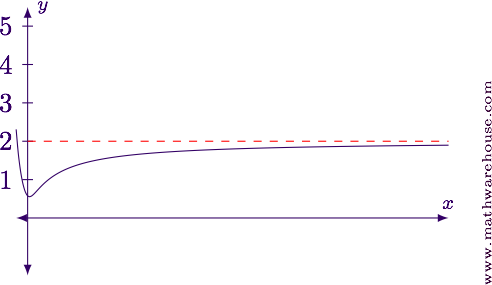
Example 5

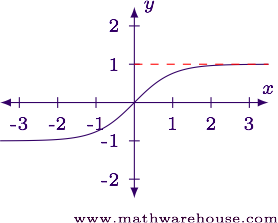
Let's look at one more example. Try using L'Hôpital's rule to evaluate $$\displaystyle \lim_{x\to\infty} \frac{e^x - e^{-x}}{e^x + e^{-x}}$$.

Attempted Solution

Step 1

Evaluate the limit in its current form.

$$ \begin{align*} \lim_{x\to\infty} \frac{e^x - e^{-x}}{e^x + e^{-x}} & = \frac{\infty - 0}{\infty + 0} = \frac \infty \infty \end{align*} $$

This limit is indeterminate, and has the correct form for L'Hôpital's rule.

Step 2

Apply L'Hôpital's rule and evaluate.

$$ \begin{align*} \lim_{x\to\infty} \frac{e^x - e^{-x}}{e^x + e^{-x}} & = \lim_{x\to\infty} \frac{\blue{\frac d {dx}\left(e^x - e^{-x}\right)}}{\red{\frac d {dx}\left(e^x + e^{-x}\right)}} = \lim_{x\to\infty} \frac{e^x + e^{-x}}{e^x - e^{-x}} = \frac \infty \infty \end{align*} $$

Notice that when we applied L'Hôpital's rule, the resulting limit was just the reciprocal of the original. We can easily see that repeated applications of the rule will just result in the function flipping over and over.

Correct Solution

Step 1

In this case, we multiply by $$e^{-x}/e^{-x}$$.

$$ \begin{align*} \lim_{x\to\infty} \frac{e^x - e^{-x}}{e^x + e^{-x}} & = \lim_{x\to\infty} \frac{\left(e^x - e^{-x}\right)}{\left(e^x + e^{-x}\right)} \cdot \frac{e^{-x}}{e^{-x}} = \lim_{x\to\infty} \frac{1 - e^{-2x}}{1 + e^{-2x}} = \frac{1 - 0}{1+ 0} = 1 \end{align*} $$

Answer

$$\displaystyle \lim_{x\to\infty} \frac{e^x - e^{-x}}{e^x + e^{-x}} = 1$$

For reference, here is the graph of the function.