What is a Limit?

Both parts of calculus are based on limits!

Example 1

Let's look at the graph of $$f(x) = \frac 4 3 x -4$$, and examine points where $$x$$ is "close" to $$x = 6$$. We'll start with points where $$x$$ is less than 6.

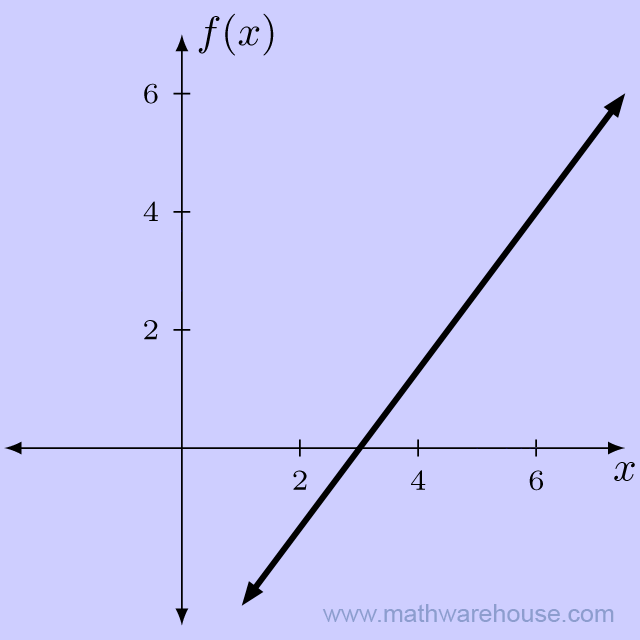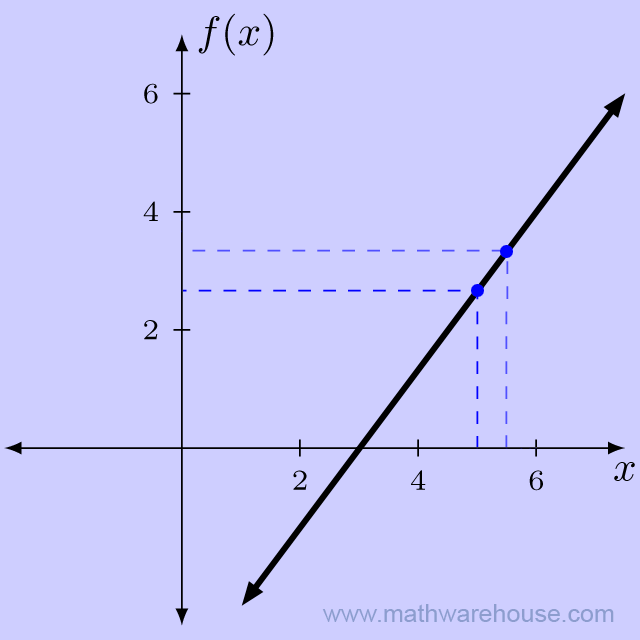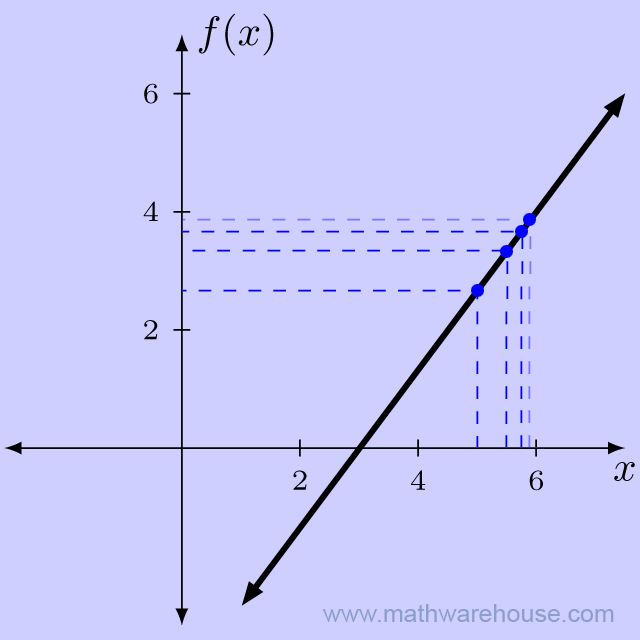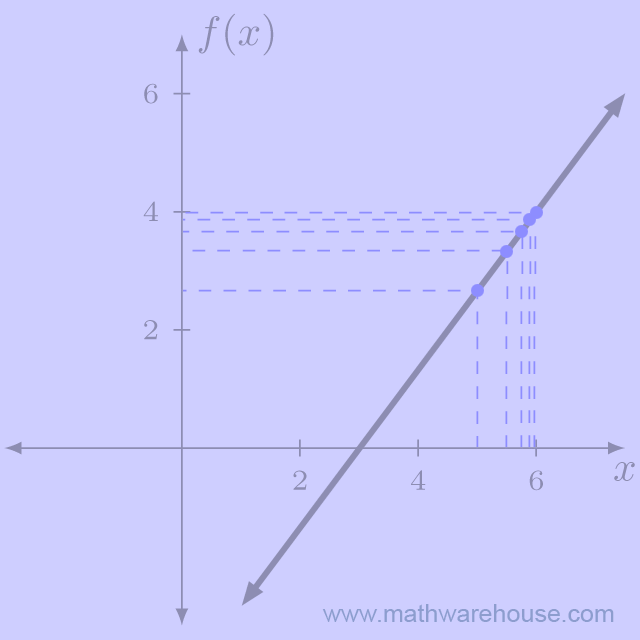
Notice that as the $$x$$-values get closer to 6, the function values appear to be getting closer to $$y = 4$$. Now, lets look at points on the function where $$x$$ is larger than 6.

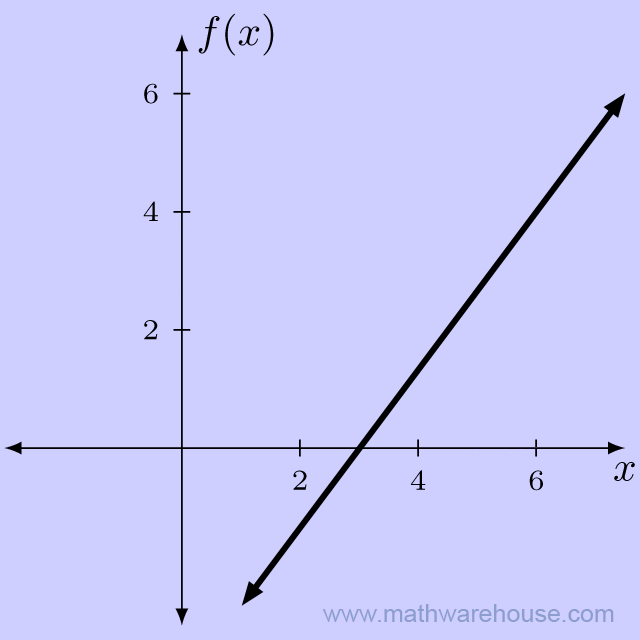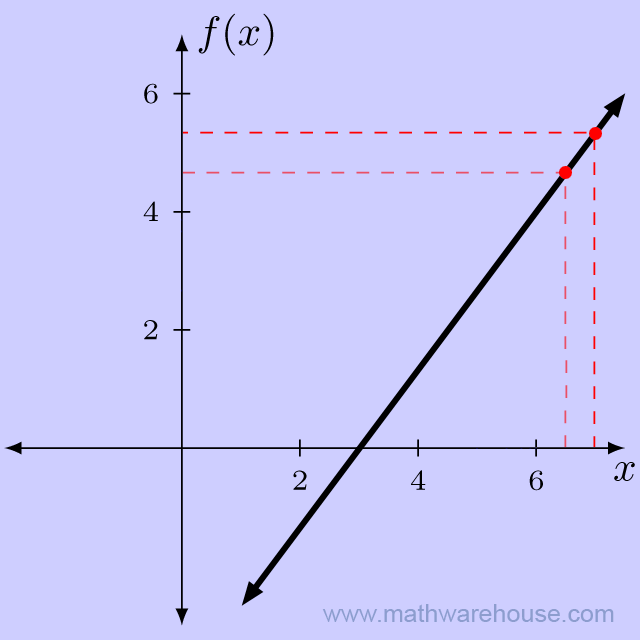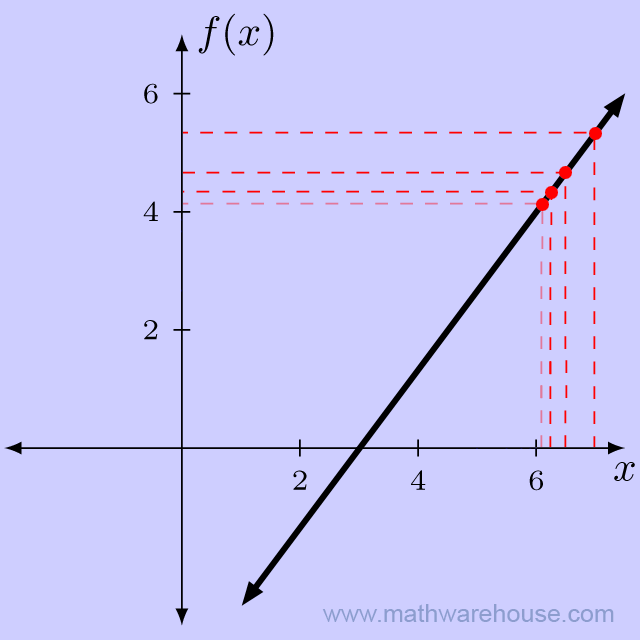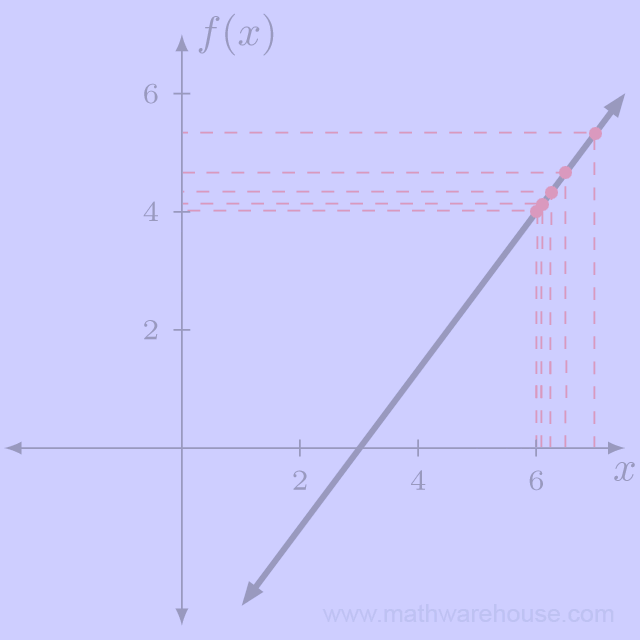
Table of Points Plotted

$$ \begin{array}{l|c} x & f(x)\\\hline \hline 7 & 5.33333\\\hline 6.5 & 4.66667\\\hline 6.25 & 4.33333\\\hline 6.1 & 4.13333\\\hline 6.01 & 4.01333\\\hline \end{array} $$

As before, the closer we got to $$x = 6$$, the closer the function got to $$y = 4$$.

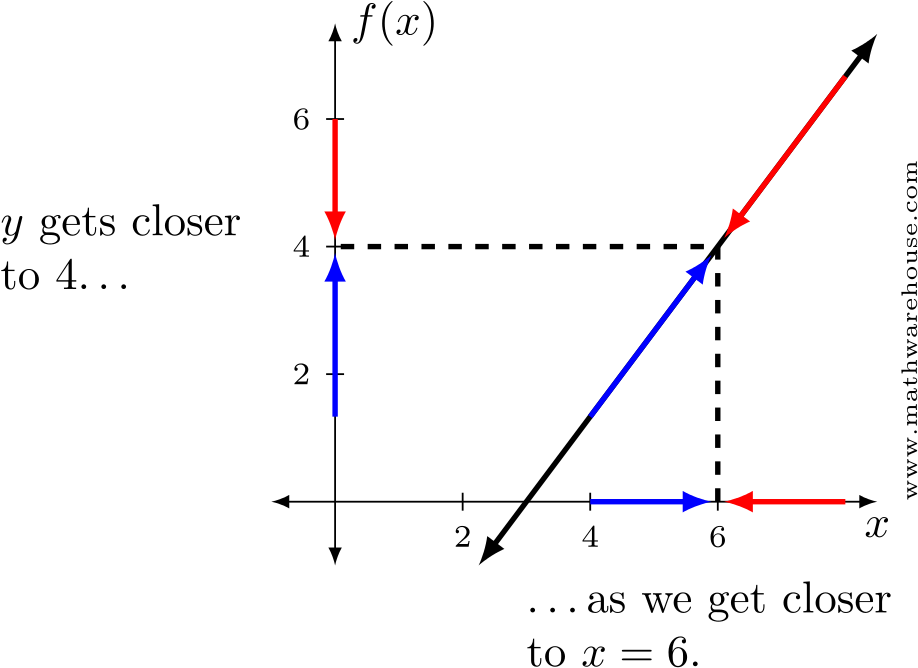
Of course, since $$f(6) = 4$$, this might not seem surprising. Nevertheless, this is the idea of a limit, and it can be summed up this way:

As $$x$$ gets closer to a particular number, what does the function get close to?

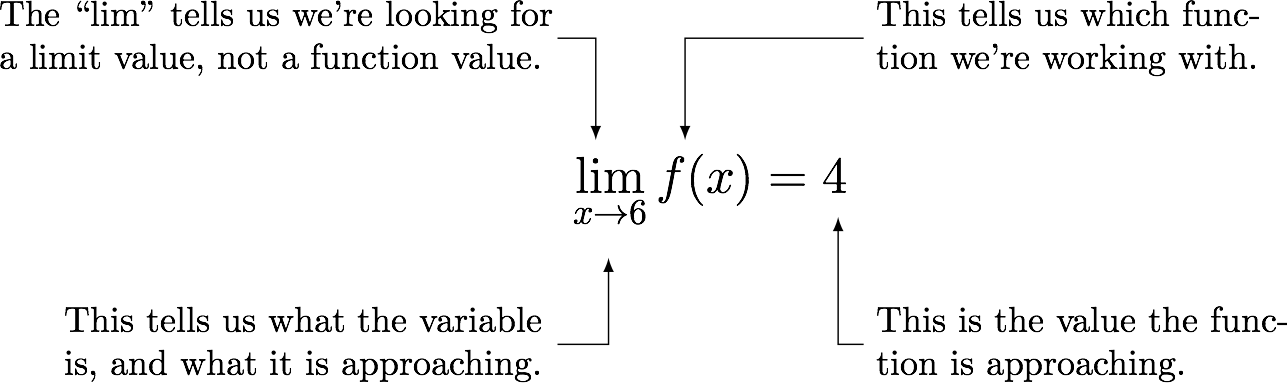
Limit Notation

Mathematicians have a special notation to indicate they are working with limit values. For example, the answer to Example 1 would be written like this:

Example 2

Suppose $$f(x) = \frac{\sin x}{x }$$. What is $$\displaystyle \lim_{x\to0} f(x)=$$?

It is tempting to just plug in $$x$$ = 0 to try to get an answer, but if we try

$$f(0) = \frac{\sin 0} {\color{red}{0}} \mbox{ is undefined! (Division by zero)}$$

Even though the function is undefined when $$x$$ = 0, we can still answer the question using the limit.

The following two tables will help us understand what happens near $$x$$ = 0.

In both tables, the closer x gets to 0, the closer the function seems to be getting to 1. Now, let’s peek at the graph of the function, just to verify it visually.

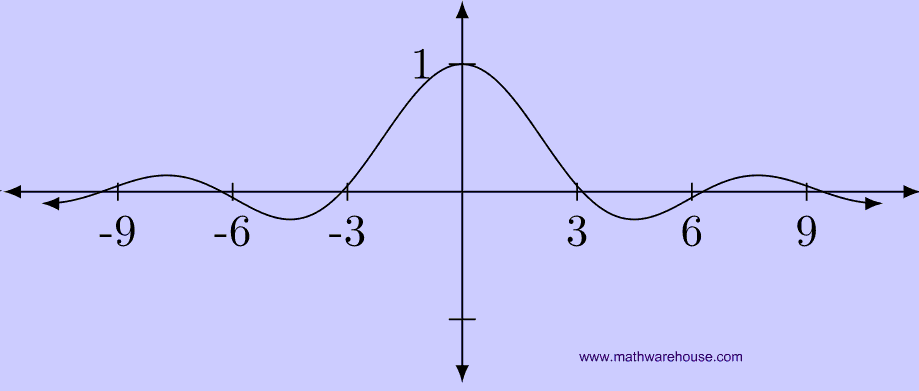
Just like the tables, the graph shows that as we get closer to $$x$$ = 0, the $$y$$-value appears to be getting closer to 1 !

Or, to use the math notation:

$$\displaystyle\lim_{x\to0}\frac{\sin x} x = 1$$.