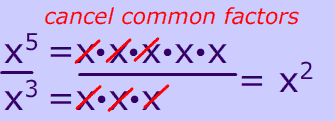Formula and Examples
$
\frac{ x^m} {x^n} = x^{m \red - n}
$
Example
$
\frac{ x^5} {x^3} = x^{5 \red - 3} = x ^2
$
Why this works
There are two ways to demonstrate the reason behind this formula
Explanation 1: If you expand the numerator and the denominator, you can see that we cancel several x's that are common factors. All that remains is $$ x \cdot x $$ which, of course, is $$ x^2 $$ .
![Example 1 - Factored explanation]()
Substract Exponents Solver
Enter any exponential equation into the algebra solver below :
Practice Problems
Use the formula for subtracting exponents to simplify each expression below.
Problem 1
Problem 2
Problem 3
Problem 4
Related:
