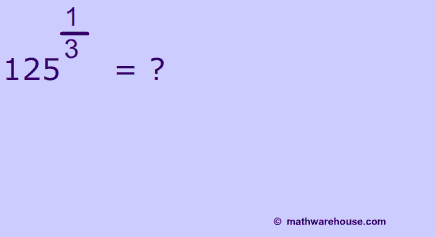Examples of Rewriting Fractional Exponents
$ \sqrt 3 = 3 ^ {\red { \frac 1 2} } $
$ \sqrt[3] 8 = 8 ^ {\red { \frac 1 3} } $
$ \sqrt[4] 81 = 81 ^ {\red { \frac 1 4} } $
Formula and examples of how to simplify Fraction exponents
$ \sqrt 3 = 3 ^ {\red { \frac 1 2} } $
$ \sqrt[3] 8 = 8 ^ {\red { \frac 1 3} } $
$ \sqrt[4] 81 = 81 ^ {\red { \frac 1 4} } $
We can use one of the laws of exponents to explain how fractional exponents work.
$ \\ 9^{\frac 1 2 } \cdot 9^{\frac 1 2 } = 9^{\frac 1 2 + \frac 1 2 } \\ = \boxed{ 9 ^1 } $
We can do the same thing with $$ \sqrt[3] 8 \cdot \sqrt[3] 8 \cdot \sqrt[3] 8 = 8 $$
$ \\ 8^{\frac 1 3} \cdot 8^{\frac 1 3 } \cdot 8^{\frac 1 3 } = 8^{\frac 1 3 + \frac 1 3+ \frac 1 3 } \\ = \boxed{ 8 ^1 } $
Below is the general formula for a fractional exponent with a numerator of 1.
$ \sqrt[n] x = x ^ {\frac 1 n} $
$$ \frac 1 n $$ is another way of asking: What number can you multiply by itself n times to get x?
Below is a specific example illustrating the formula for fraction exponents when the numerator is not one. There are two ways to simplify a fraction exponent such $$ \frac 2 3$$ . You can either apply the numerator first or the denominator. See the example below.
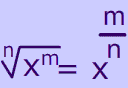 Example
Example