The formula
$$ \text{Area } =\frac{1}{2} \cdot c \cdot b \cdot sin(\text{A}) $$
or, in general
$$ Area = \frac{1}{2} \cdot side_1 \cdot side_2 \cdot sin(\text{included angle}) $$
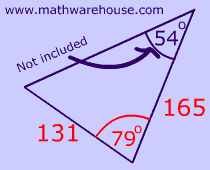
Visit this url, if you want to review what is meant by 'included angle'.
Where does this formula come from?
Answer
We all know that the general formula for the area of a triangle is $$A= \frac{1}{2} \cdot base \cdot height $$.
Well, look at the picture below, the question is, how do we get the height of the triangle?
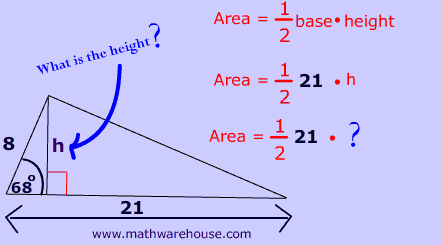
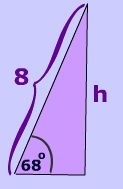
Well, we can use sine to solve for the side length.
$$
sin(68) = \frac{h}{8}
$$
$$
h = 8 \cdot sin(68)
$$
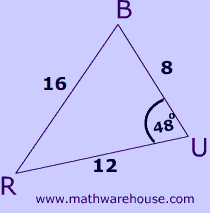
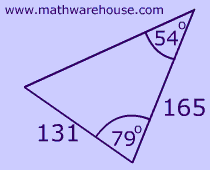
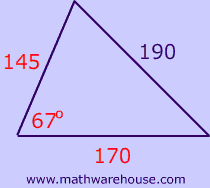
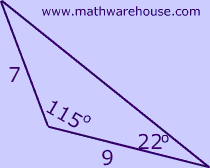
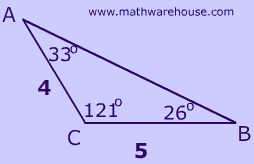
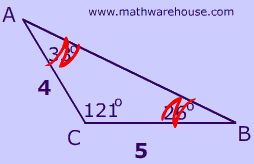
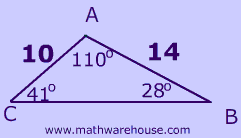
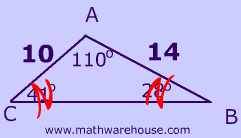
Can you identify which triangle below has an included angle?
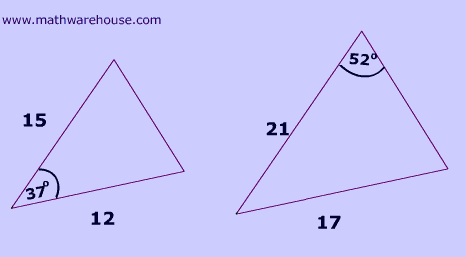
Example 1
Identify two sides and the included angle!
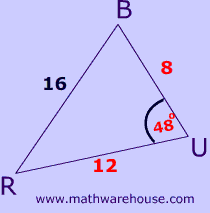
Apply the formula!
$$ A = \frac{1}{2} \cdot c\cdot b\cdot sin(A) \\ A = \frac{1}{2} \cdot 8 \cdot 12 \cdot sin(48) \\ = 3.567 $$