How does SOHCAHTOA help us find side lengths?
Example of finding Side Length
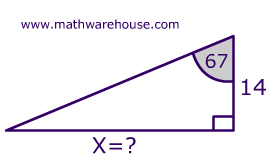
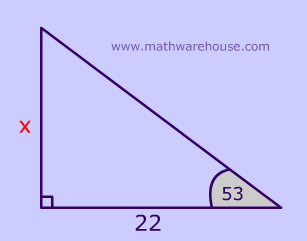
How to use sine, cosine, tangent to calculate x from diagram 1.
Diagram 1
![example problem]() Step 1
Step 1
Write a table listing the givens and what you want to find:
| Givens |
Want to Find |
| $$67 ^{\circ} $$ |
Opposite |
| adjacent |
|
Step 2
Based on your givens and unknowns, determine which sohcahtoa ratio to use.
In this case we want to use tangent because it's the ratio that involves the adjacent and opposite sides.
Step 3
Set up an equation based on the ratio you chose in the step 2.
$
tan(67) = \frac{opp}{adj}
\\
tan(67) = \frac{ \red x}{14}
$
Step 4
Solve the equation for the unknown.
$
tan(67) = \frac{ \red x}{14}
\\
14\times tan(67) = \red x
\\
x \approx 32.98
$
![]() After you are comfortable writing sine, cosine, tangent ratios you will often use sohcahtoa to find the sides of a right triangle. That is exactly what we are going to learn .
After you are comfortable writing sine, cosine, tangent ratios you will often use sohcahtoa to find the sides of a right triangle. That is exactly what we are going to learn .