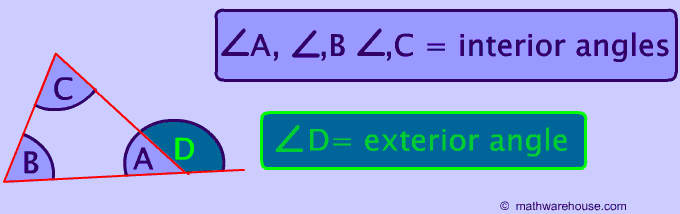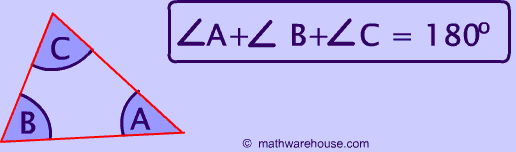Triangles Side and Angles

Properties of Triangles

Triangles are one of the most fundamental geometric shapes and have a variety of often studied properties relating to their

• (1)interior angles (angles on the inside) sum up to 180° (more)
• (2) Triangle Inequality Theorem : This theorem states that the sum of the lengths of any 2 sides of a triangle must be greater than the third side (more)
• (3)Relationship between measurement of the sides and angles in a Triangle: The largest interior angle and side are opposite each other. The same rule applies to the smallest sized angle and side and the middle sized angle and side. (more)

What is the difference between interior and exterior angles of a triangle?

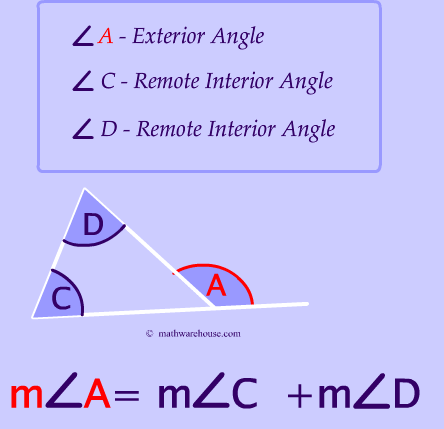
This question is answered by the picture below. You create an exterior angle by extending any side of the triangle. Web page on the relationship between exterior and interior angles of a triangle

Interior Angles of a Triangle Rule

This may be one the most well known mathematical rule--The sum of all 3 interior angles in a triangle is 180°. As you can see from the picture below, if you add up all of the angles in a triangle the sum must equal 180°. This property of a triangle's interior angles is simply a specific example of the general rule for any polygon's interior angles.

To explore the truth of this rule, try Math Warehouse's interactive triangle, which allows you to drag around the different sides of a triangle and explore the relationship between the angles and sides. No matter how you position the three sides of the triangle, the total degrees of all interior angles (the three angles inside the triangle) is always 180°.

Interactive Demonstration of Interior Angle Sum

What is mLNM in the triangle below?

Answer

LMN = 34° MLN = 29°

Use the rule for interior angles of a triangle: mLNM +mLMN +mMLN =180° mLNM +34° + 29° =180° mLNM +63° =180° mLNM = 180° - 63° = 117°

A triangle's interior angles are HOP, HPO and PHO.
HOP is 64° and mHPO is 26°.
What is mPHO?

Answer

Use the interior angles of a triangle rule :
mPHO = 180° - 26° -64° = 90°

Relationship between Side Lengths and Angle Measurements

Worksheet on the relationship between the side lengths and angle measurements of a triangle

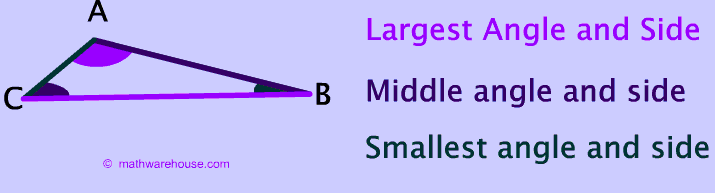
In any triangle,
• the largest interior angle is opposite the largest side.
• the smallest interior angle is opposite the smallest side
• the middle-sized interior angle is opposite the middle-sized side

To explore the truth of the statements you can use Math Warehouse's interactive triangle, which allows you to drag around the different sides of a triangle and explore the relationships betwen the measures of angles and sides. No matter how you position the three sides of the triangle, you will find that the statements in the paragraph above hold true.(All right, the isosceles and equilateral triangle are exceptions due to the fact that they don't have a single smallest side or, in the case of the equilateral triangle, even a largest side. Nonetheless, the principle stated above still holds true. !)

Interactive Demonstration of Side Length vs Angle Measure