Use The Quadratic Formula Calculator to see Quadratic Formula and discriminant in Action! This calculator will solve any quadratic equation you type in (even if solutions are imaginary).
Pre Requisite Knowledge
To understand what the discriminant does, it's important that you have a good understanding of:
Pre Req 2 : What is the solution of a quadratic equation:
The solution can be thought of in two different ways.
- Algebraically, the solution occurs when y = 0. So the solution is where $$y =\red ax^2 + \blue bx + \color{green} c $$ becomes $$0 =\red ax^2 + \blue bx + \color{green} c $$.
- Graphically, since y = 0 is the x-axis, the solution is where the parabola intercepts the x-axis. (This only works for real solutions).
In the picture below, the left parabola has 2 real solutions (red dots), the middle parabola has 1 real solution (red dot) and the right most parabola has no real solutions (yes, it does have imaginary ones).
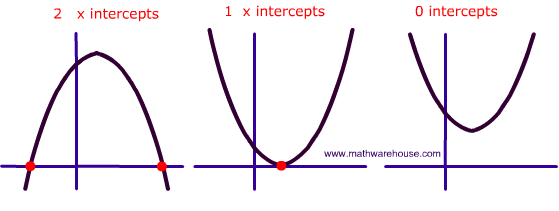
What does the discriminant look like?
It looks like .. a number.
5, 2, 0, -1 - each of these numbers is the discriminant for 4 different quadratic equations.
What is the discriminant anyway?
The discriminant is a number that can be calculated from any quadratic equation.
A quadratic equation is an equation that can be written as $$ ax^2 + bx + c $$ (where $$a \ne 0 $$).
What is the formula for the Discriminant?
The discriminant for any quadratic equation of the form $$ y =\red a x^2 + \blue bx + \color {green} c $$ is found by the following formula and it provides critical information regarding the nature of the roots/solutions of any quadratic equation.
$ \boxed{Formula} \\ \text{Discriminant } = \blue b^2 -4 \red a \color{green} c $
$ \boxed{Example} \\ \text{Equation :} y =\red 3 x^2 + \blue 9x + \color {green} 5 \\ \text{Discriminant } = \blue 9^2 -4 \cdot \red 3 \cdot \color{green} 5 \\ \text{Discriminant } = \boxed{ 6} $
What does this formula tell us?
The discriminant tells us the following information about a quadratic equation:
- If the solution is a real number or an imaginary number.
- If the solution is rational or if it is irrational.
- If the solution is one unique number or two different numbers.
Nature of the Solutions
| Value of the discriminant | Type and number of Solutions | Example of graph |
|---|---|---|
|
$ b^2 - 4ac > 0 $ $ \text{Example :} \\ y = \red 3x^2 \blue{-6}x + \color{green} 2 \\ \text{Discriminant} \\ \blue{-6}^2 - 4 \cdot \red 3 \cdot \color{green} 2 \\ = \boxed{12} \\ $ |

If the discriminant is a positive number, then there are 2 real solutions. This means that the graph of the parabola interepts the x-axis at 2 distinct points . |
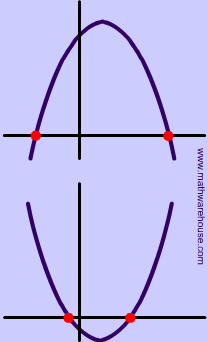
|
|
$ \text{Example :} \\ y = \red 3x^2 + \blue 4 x \color{green} {-4} \\ \text{Discriminant} \\ \blue 4^2 - 4 \cdot \red 3 \cdot \color{green} {-4} \\ = \boxed{64} \\ $ |

If the discriminant is positive and also a perfect square like 64, then there are 2 real rational solutions. |
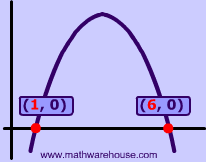
|

$ \text{Example :} \\ y = \red 3x^2 \blue {-6} x + \color{green} 2 \\ \text{Discriminant} \\ \blue {-6}^2 - 4 \cdot \red 3 \cdot \color{green} 2 \\ = \boxed{12 } \\ $ |

If the discriminant is positive and not a perfect square like 12, then there are 2 real irrational solutions. |
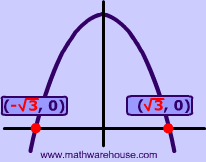
|

$ b^2 - 4ac = 0 $ $ \text{Example :} \\ y = \red 4 x^2 \blue{-28}x + \color{green} {49} \\ \text{Discriminant} \\ \blue{-28}^2 - 4 \cdot \red 4 \cdot \color{green} 49 \\ = \boxed{0} \\ $ |

|
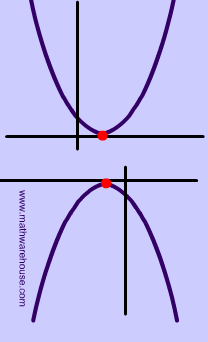
|

$ b^2 - 4ac < 0 $ $ \text{Example :} \\ y = \red x^2 \blue{-3}x + \color{green} 4 \\ \text{Discriminant} \\ \blue{-3}^2 - 4 \cdot \red 1 \cdot \color{green} 4 \\ = \boxed{-7} \\ $ |

There are only imaginary Solutions. This means that the graph of the quadratic never intersects the axes. |
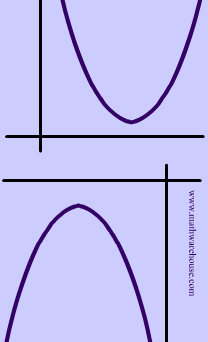
|
Example
Quadratic Equation: $$ y = x^2 + 2x + 1$$
$ a = \red 1 \\ b = \blue 2 \\ a = \color{green} {1} $
The discriminant for this equation is:
$ \text{Discriminant } = \blue b^2 -4 \red a \color{green} c \\ \text{Discriminant } = \blue 2^2 -4 \cdot \red 1 \cdot \color{green} \cdot 1 \\ \text{Discriminant } = 4 -4 \\ \text{Discriminant } = \boxed{0} \\ $
Since the discriminant is zero, there should be 1 real solution to this equation.
Below is a picture representing the graph and the one solution of $$ y = x^2 + 2x + 1$$.
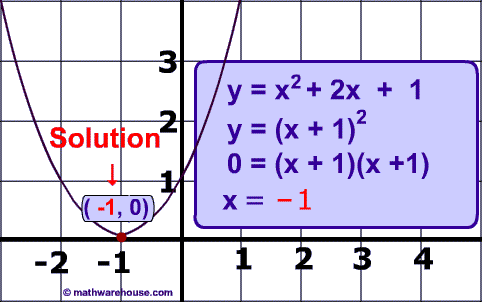
Practice Problems
Practice 1
In this quadratic equation, $$ y =\red 1 x^2 + \blue {-2} + \color {green} 1 $$
$ \text{Equation : } y =\red 1 x^2 + \blue {-2}x + \color {green} 1 \\ a = \red 1 \\ b = \blue{-2} \\ c = \color{green} 1 $
Using our general formula:
$$ \text{Discriminant } \\ \begin{aligned} &= \blue b^2 -4 \cdot \red a \cdot \color{green} c \\ &= \blue {-2}^2 -4 \cdot \red 1 \cdot \color{green} 1 \\ &= \boxed{0} \end{aligned} $$
Since the discriminant is zero, we should expect 1 real solution which you can see pictured in the graph below.
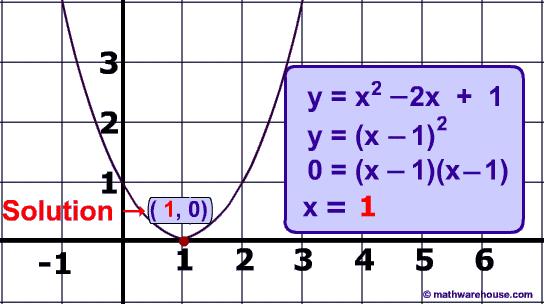
Practice 2
In this quadratic equation, $$ y =\red 1 x^2 + \blue {-1}x + \color {green} 1 $$
$ \text{Equation : } y =\red 1 x^2 + \blue {-1} + \color {green} 1 \\ a = \red 1 \\ b = \blue{-1} \\ c = \color{green} {2} $
Using our general formula:
$$ \text{Discriminant } \\ \begin{aligned} &= \blue b^2 -4 \cdot \red a \cdot \color{green} c \\ &= \blue {-1}^2 -4 \cdot \red 1 \cdot \color{green} {-2} \\ &= 1 - -8 \\ &= 1 + 8 = \boxed 9 \end{aligned} $$
Since the discriminant is positive and rational, there should be 2 real rational solutions to this equation. As you can see below, if you use the quadratic formula to find the actual solutions, you do indeed get 2 real rational solutions.
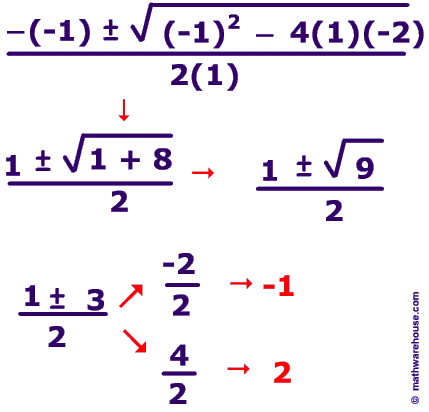
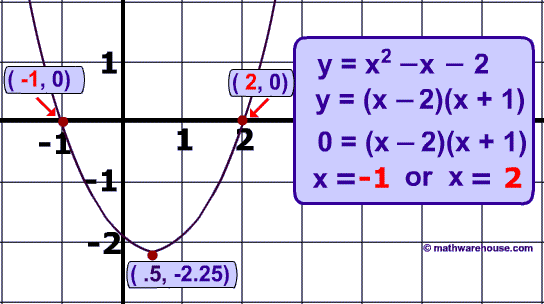
Practice 3
In this quadratic equation, y = 1x² − 1.
- a = 1
- b = 0
- c = − 1
$$ \color{Red}{b^2} - 4\color{Magenta}{a}\color{Blue}{c} \\ \color{Red}{(0)^2} - 4\color{Magenta}{(1)}\color{Blue}{(-1)} = 4 $$
Since the discriminant is positive and a perfect square, we have two real solutions that are rational.
Again if you'd like to see the actual solutions and the graph, just look below:
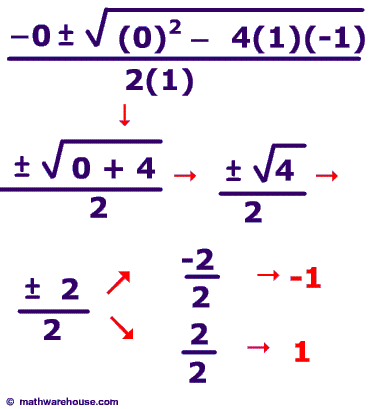
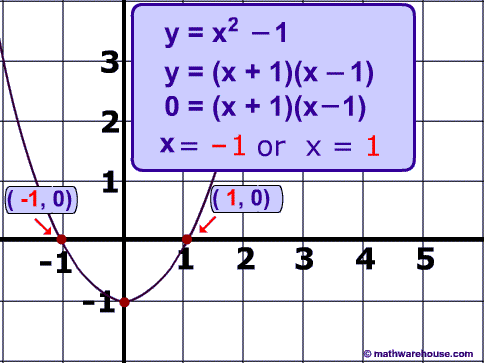
Practice 4
In this quadratic equation, y = x² + 4x − 5.
- a = 1
- b = 4
- c = − 5
$$ \color{Red}{b^2} - 4\color{Magenta}{a}\color{Blue}{c} \\ \color{Red}{(4)^2} - 4\color{Magenta}{(1)}\color{Blue}{(-5)} \\ 16 - 4(-5) = 16 +20 \\ = 36 $$
Since this quadratic equation's discriminant is positive and a perfect square, there are two real solutions that are rational.
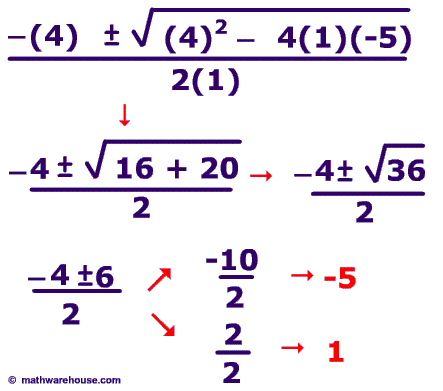
Practice 5
In this quadratic equation, y = x² - 4x + 5.
- a = 1
- b = -4
- c = 5
$$ \color{Red}{b^2} - 4\color{Magenta}{a}\color{Blue}{c} \\ \color{Red}{(-4)^2} - 4\color{Magenta}{(1)}\color{Blue}{(5)} \\ = 16 - 20 = -4 $$
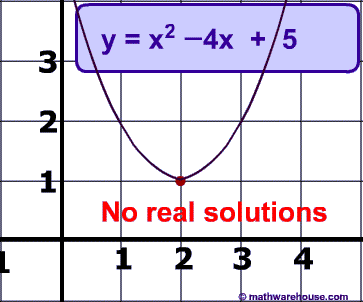
Since the discriminant is negative, there are no real solutions to this quadratic equation. The only solutions are imaginary.
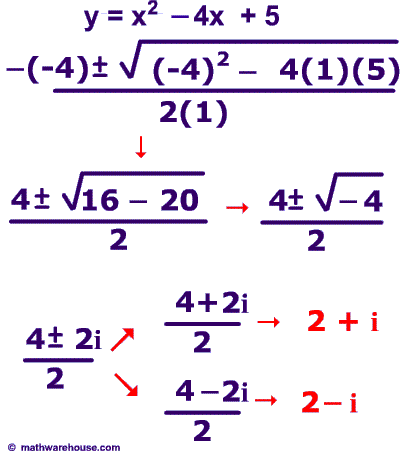
Below is a picture of this quadratic's graph.
Practice 6
y = x² + 4
- a = 1
- b = 0
- c = 4
$$ \color{Red}{b^2} - 4\color{Magenta}{a}\color{Blue}{c} \\ \color{Red}{(0)^2} - 4\color{Magenta}{(1)}\color{Blue}{(4)} = -16 $$
Since the discriminant is negative, there are two imaginary solutions to this quadratic equation.
The solutions are 2i and -2i.
Below is a picture of this equations graph.

Practice 7
y = x² + 25
- a = 1
- b = 0
- c = 25
$$ \color{Red}{b^2} - 4\color{Magenta}{a}\color{Blue}{c} \\ \color{Red}{(0)^2} - 4\color{Magenta}{(1)}\color{Blue}{(25)} = -100 $$
Since the discriminant is negative, there are two imaginary solutions to this quadratic equation.
The solutions are 5i and -5i.















