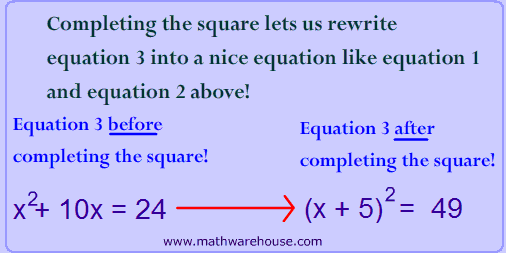Completing the Square in math: The easy way. Examples and practice problems. All that you do is...| Math Warehouse

The goal of this web page is to explain how to complete the square, how the formula works and provide lots of practice problems.
On a different page, we have a completing the square calculator which does all the work for this topic. You just enter the quadratic.

What does "completing the square" do for us?

It gives us a way to find the last term of a perfect square trinomial.

Okay, what is a "perfect square trinomial"??

A perfect square trinomial is a polynomial that you get by squaring a binomial. (binomials are things like 'x + 3' or 'x − 5').

Examples of perfect square trinomials

$$ x^2 + 2x + 1$$ This is a perfect square trinomial because it equals $$(x + 1)^2$$.
$$x^2 + 4x + 4$$ This is a perfect square trinomial because it equals $$(x + 2)^2$$.
$$x ^2 + 6x + 9 $$ This is a perfect square trinomial because it equals $$(x + 3)^2$$.

Non Examples

These are NOT perfect square trinomials.

$$x ^2 + 3x + 2 $$ This is not a perfect square trinomial because it equals $$ (x + 1)(x + 2) $$.
$$x ^2 + 7x + 10 $$ This is not a perfect square trinomial because it equals $$ (x + 2)(x + 5) $$.
$$ x ^2 - 9$$ This is not a perfect square trinomial because it equals $$ (x \red{+} 3) (x \red{-} 3) $$.

So, what does it really do for us?

Before we look at the answer, let's first examine the three equations below. How would you solve each one?

Equation 1

$$ x^2 = 25 $$

$$\sqrt{x^2} = \sqrt{25} \\ x = \pm 5 $$

Equation 2

$$ (x + 1) ^2 = 36 $$

$$\sqrt{(x + 1)^2} = \sqrt{36} \\ x + 1= \pm 6 \\ x = 5 \text{ or }-7 $$

Equation 3

$$ x^2 +10x = 24 $$

The rest of this web page will try to show you how to complete the square.

Now, you might be saying to yourself that $$ x^2 + 10x = 24 $$ could easily be solved without any fancy new methods. (You could easily factor it, for instance.)
And, this of course is true. However, it turns out there are times when completing the square comes in very handy and will help you do a variety of things including convert the equations of circles, hyperbolas, ellipses into forms that make it much easier to work with these shapes.

If you haven't heard of these conic sections yet,don't worry about it. But, trust us, completing the square can come in very handy and can make your life much easier when you have to deal with certain types of equations.

Formula for Completing the Square

To best understand the formula and logic behind completing the square, look at each example below and you should see the pattern that occurs whenever you square a binomial to produce a perfect square trinomial.

Practice Problems

Directions Find the missing value to complete the square.

Problem 1

$$x^2 + \red{16}x + \blacksquare $$

Step 1

Divide the middle term by 2.

$$ \\ \frac{ \red{16} }{ \color{green}{2} }= \blue{8} $$

Step 2

Then square the result.

$$ \blue{8}^2 = 64 $$

Step 3

Final Answer! : $$ x^2 + \red{16}x + 64 $$

You can always check your work by seeing by foiling the answer to step 2 and seeing if you get the correct result.

$$ (x+ \blue{8}) = x^2 + \red{16}x + 64 $$.

Problem 2

$$x^2 + \red{20}x + \blacksquare $$

Step 1

Divide the middle term by 2.

$$ \\ \frac{ \red{20} }{ \color{green}{2} }= \blue{10} $$

Step 2

Then square the result.

$$ \blue{10}^2 = 100 $$

Step 3

Final Answer! : $$ x^2 + \red{20}x + 100 $$

You can always check your work by seeing by foiling the answer to step 2 and seeing if you get the correct result.

$$ (x+ \blue{ 10 }) =x^2 + \red{20}x + 100 $$.

Problem 3

$$ x^2 + \red{18}x + \blacksquare $$

Step 1

Divide the middle term by 2.

$$ \\ \frac{ \red{18} }{ \color{green}{2} }= \blue{9} $$

Step 2

Then square the result.

$$ \blue{9}^2 = 81 $$

Step 3

Final Answer!: $$ x^2 + \red{18}x + 81 $$.

You can always check your work by seeing by foiling the answer to step 2 and seeing if you get the correct result.

$$ (x+ \blue{ 9 }) =x^2 + \red{18}x + 81 $$.

Problem 4

$$x^2 + \red{5}x + \blacksquare $$

Step 1

Divide the middle term by 2.

$$ \\ \frac{ \red{5} }{ \color{green}{2} }= \blue{ \frac{5}{2} } $$

Step 2

Then square the result.

$$ \left(\blue{\frac{5}{2}} \right)^2 = \frac{25}{4} $$

Step 3

Final Answer!: $$ x^2 + \red{5}x + \frac{25}{4} $$.

You can always check your work by seeing by foiling the answer to step 2 and seeing if you get the correct result.

$$ (x+ \blue{ \frac{5}{2} }) = x^2 + \red{5}x + \frac{25}{4} $$

Problem 5

$$ x^2 + \red{7}x + \blacksquare $$

Step 1

Divide the middle term by 2.

$$ \\ \frac{ \red{7} }{ \color{green}{2} }= \blue{ \frac{7}{2} } $$

Step 2

Then square the result.

$$ \left(\blue{\frac{7}{2}} \right)^2 = \frac{49}{4} $$

Step 3

Final Answer!: $$ x^2 + \red{7}x + \frac{49}{4} $$.

You can always check your work by seeing by foiling the answer to step 2 and seeing if you get the correct result.

$$ (x+ \blue{ \frac{7}{2} }) =x^2 + \red{7}x + \frac{49}{4} $$.

II. Completing Square when a is not 1

What about $$ \blue{3}x^2+18x $$, what then ?

Practice Problems

Problem 6

$$ 2x^2 + 12x + \blacksquare $$

Step 1

Factor out any common factors.

$$ \red{2} (\color{darkgreen}{x^2 + 6x}) $$

Step 2

Divide the middle term by 2 then square it (like in the first set of practice problems.

$$ \frac{ 6}{ 2} = 3 \\ 3^2 = 9 $$

Step 3

Substitute into equation and distribute.

$$ \red{2} (x^2 + 6x + 9) \\ \red{2} x^2 + \red{2} \cdot 6x + \red{2} \cdot 9 \\ 2x^2 + 12x + 18 $$

Problem 7

$$ 3x^2 + 36x + \blacksquare $$

Step 1

Factor out any common factors.

$$ \red{3} (\color{darkgreen}{x^2 + 12x}) $$

Step 2

Divide the middle term by 2 then square it (like in the first set of practice problems.

$$ \frac{ 12}{ 2} = 6 \\ 6^2 = 36 $$

Step 3

Substitute into equation and distribute.

$$ \red{3} (x^2 + 12x + 36) \\ \red{3} x^2 + \red{3} \cdot 12x + \red{3} \cdot 36 \\ 3x^2 + 36x + 108 $$

Problem 8

$$ 5x^2 + 20x + \blacksquare $$

Step 1

Factor out any common factors.

$$ \red{5} (\color{green}{x^2 + 4x}) $$

Step 2

Divide the middle term by 2 then square it (like in the first set of practice problems.

$$ \frac{ 4}{ 2} = 2 \\ 2^2 = 4 $$

Step 3

Substitute into equation and distribute.

$$ \red{5} (x^2 + 4x + 4) \\ \red{5} x^2 + \red{5} \cdot 4x + \red{5} \cdot 4 \\ 5x^2 + 20x + 20 $$

The next problems are quite challenging, good luck!

Problem 9

$$ 2ax^2 + 12ax + \blacksquare $$

Step 1

Factor out any common factors.

$$ \red{2a} (\color{darkgreen}{x^2 + 6x}) $$

Step 2

Divide the middle term by 2 then square it (like in the first set of practice problems.

$$ \frac{ 6}{ 2} = 3 \\ 3^2 = 9 $$

Step 3

Substitute into equation and distribute.

$$ \red{2a} (x^2 + 6x + 9) \\ \red{2a} x^2 + \red{2a} \cdot 6x + \red{2a} \cdot 9 \\ 2ax^2 + 12ax + 18a $$

Problem 10

$$ 3x^3 + 18x^2 + \blacksquare $$

Step 1

Factor out any common factors.

$$ \red{3x} (\color{darkgreen}{x^2 + 6x}) $$

Step 2

Divide the middle term by 2 then square it (like in the first set of practice problems.

$$ \frac{ 6}{ 2} = 3 \\ 3^2 = 9 $$

Step 3

Substitute into equation and distribute.

$$ \red{3x} (x^2 + 6x + 9) \\ \red{3x} \cdot x^2 + \red{3x} \cdot 6x + \red{3x} \cdot 9 \\ 3x^3 + 18x^2 + 27x $$

Problem 11

$ 4x^3 + 2x^2 + \blacksquare $

Step 1

Factor out any common factors.

$$ \red{4x} (\color{darkgreen}{x^2 + \frac{1}{2}x}) $$

Step 2

Divide the middle term by 2 then square it (like in the first set of practice problems.

$$ \frac{1}{2} \div 2 = \frac{1}{4} \\ \left(\frac{1}{4} \right)^2 = \frac{1}{16} $$

Step 3

Substitute into equation and distribute.

$$ \red{4x} (x^2 + \frac{1}{2}x + \frac{1}{16}) \\ \red{4x} \cdot x^2 + \red{4x} \cdot \frac{1}{2}x+ \red{4x} \cdot \frac{1}{16} \\ 4x^3 + 2x^2 + \frac{4}{16} x \\ 4x^3 + 2x^2 + \frac{1}{4} x $$

Worksheet on Completing the Square

Completing Square Calculator