Part I.
Simplifying Powers of $$i$$
$$ i^5 = ? \\ i ^ {21} = ? $$
This PageWhat is an imaginary number anyway?
Imaginary numbers are based on the mathematical number $$ i $$.
$$ i \text { is defined to be } \sqrt{-1} $$
From this 1 fact, we can derive a general formula for powers of $$ i $$ by looking at some examples.
Table 1$ \text{ Table 1} \\ \begin{array}{ccc|c} \hline Expression & & Work & Result \\\hline \red{i^ \textbf{2}} & = & i \cdot i = \sqrt{-1} \cdot \sqrt{-1} & \red{ \textbf{ -1 }} \\\hline \red{i^ \textbf{3}} & = & i^2 \cdot i = -1 \cdot i & \red{ \textbf{-i} } \\\hline \red{ i^ \textbf{4} } & = & i^2 \cdot i^2 -1 \cdot -1 = & \red{1} \\\hline \end{array} $
You should understand Table 1 above .
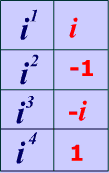
Table 1 above boils down to the 4 conversions that you can see in Table 2 below. You should memorize Table 2 below because once you start actually solving problems, you'll see you use table 2 over and over again!
Table 2
$
\text{ Table 2}
$
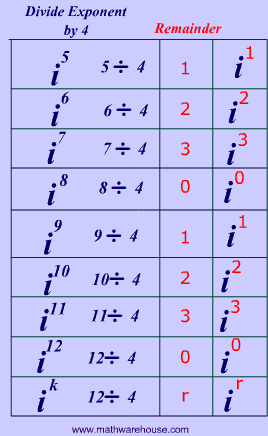
What is the larger pattern?
In order to understand how to simplify the powers of $$ i $$, let's look at some more examples, and we'll soon see a formula emerge!
$ \begin{array}{c|c|c} Expression & Work & Result \\\hline \red{i^ \textbf{5}} & \blue{i^4} \cdot i^1 = \blue{1} \cdot i & \red{ \textbf{ i }} \\\hline \red{i^ \textbf{6}} & \blue{i^4} \cdot i^2= \blue{1} \cdot -1 & \red{ \textbf{-1}} \\\hline \red{ i^ \textbf{7} } & \blue{ i^4} \cdot i^3 =\blue{1} \cdot -i & \red{ \boldsymbol{ -i}} \\\hline \red{ i^ \textbf{8} } & = \blue{ i^4} \cdot \blue{ i^4}= \blue{1} \cdot \blue{1} = & \red{ \textbf{ 1}} \\\hline \end{array} $
Do you see the pattern yet? Let's look at 4 more and then summarize.
$
\begin{array}{c|c|c}
Expression & Work & Result \\\hline
\red{i^ \textbf{9}} & = \blue{i^4} \cdot \blue{i^4} \cdot i^1 = \blue{1} \cdot \blue{1} \cdot i = & \red{ \textbf{ i }} \\\hline
\red{i^ \textbf{10}} & = \blue{i^4} \cdot \blue{i^4} \cdot i^2 = \blue{1} \cdot \blue{1} \cdot i^2 = & \red{ \textbf{ -1 }} \\\hline
\red{i^ \textbf{11}} & = \blue{i^4} \cdot \blue{i^4} \cdot i^3 = \blue{1} \cdot \blue{1} \cdot i^3 = & \red{ \textbf{ -i }} \\\hline
\red{i^ \textbf{12}} & = \blue{i^4} \cdot \blue{i^4} \cdot \blue{i^4} = \blue{1} \cdot \blue{1} \cdot \blue{1}= & \red{ \textbf{ 1 }} \\\hline
\end{array}
$
The General Formula
$$ i^k$$ is the same as $$ i^\red{r} $$ where $$ \red{r} $$ is the remainder when k is divided by 4.
Whether the remainder is 1, 2, 3, or 4, the key to simplifying powers of i is the remainder when the exponent is divided by 4.
Practice Problems
Problem 1
Problem 2
Problem 3
Problem 4
Problem 5
Remember your order of operations. Exponents must be evaluated before multiplication so you can think of this problem as $$ 5 \cdot (\color{Blue}{i^ {22}}) $$
Step 1Calculate the remainder
$$ 22 \div 4 $$ has a remainder of $$ \red{2} $$
Step 2
Rewrite
$$ i^{ \red{2}} $$
Step 3
Simplify using Table2
$$ i^{ \red{2}} = -1 $$
Step 4
$$ 5 \cdot ( {\color{Blue}-1} ) = -5 $$
Problem 6
Remember your order of operations. Exponents must be evaluated before multiplication so you can think of this problem as $$ 12 \cdot ( {\color{Blue}i^ {36}}) $$
Step 1Calculate the remainder
$$ 36 \div 4 $$ has a remainder of $$ \red{0} $$
Step 2
Rewrite
$$ i^{ \red{0}} $$
Step 3
Simplify using Table2
$$ i^{ \red{0}} = 1 $$
Step 4
$$ 12 \cdot ( {\color{Blue} 1} ) = 12 $$
Problem 7
Remember your order of operations. Exponents must be evaluated before multiplication so you can think of this problem as $$ 7 \cdot ( {\color{Blue}i^ {103}}) $$
Step 1Calculate the remainder
$$ 103 \div 4 $$ has a remainder of $$ \red{3} $$
Step 2
Rewrite
$$ i^{ \red{3}} $$
Step 3
Simplify using Table2
$$ i^{ \red{3}} = -i $$
Step 4
$$ 7 \cdot ( {\color{Blue} -i} ) = -7i $$
Further Reading:
