A+

A−

Home

Graphing Calc

Algebra

Math Games

Geometry

Interactive

Trigonometry

Scientific Calc

Home

Graphing Calc

Algebra

Math Games

Geometry

Interactive

Trigonometry

Scientific Calc

Home

Graphing Calc

Algebra

Math Games

Geometry

Interactive

Trigonometry

Scientific Calc

Pythagorean Theorem

How to Use The Pythagorean Theorem

Free Triangle Worksheets

Pythagorean Theorem Calculator | Right Triangle Images

The Formula

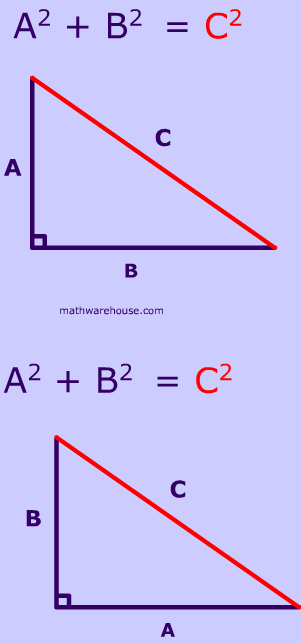
The picture below shows the formula for the Pythagorean theorem. In the pictures below, side C is always the hypotenuse. Remember that this formula only applies to right triangles.

Examples of the Pythagorean Theorem

When you use the Pythagorean theorem, just remember that the hypotenuse is always 'C' in the formula above . Look at the following examples to see pictures of the formula.

Video Tutorial on How to Use the Pythagorean Theorem

Step By Step Examples of Using the Pythagorean Theorem

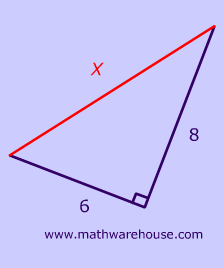
Example 1 (solving for the hypotenuse)

Use the Pythagorean theorem to determine the length of X

Step 1) Identify the legs and the hypotenuse of the right triangle.

The legs have length '6 and '8' . 'X' is the hypotenuse because it is opposite the right angle. See Picture

Step 2) Substitute values into the formula (remember 'c' is the hypotenuse)	A² + B² = C² 6² + 8² = X²
Step 3) Solve for the unknown

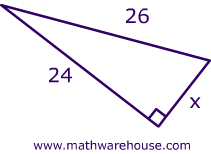
Example 2 (solving for a Leg)

Use the Pythagorean theorem to determine the length of X

Step 1) Identify the legs and the hypotenuse of the right triangle.

The legs have length '24' and 'X' are the legs. The hypotenuse is 26. See Picture

Step 2) Substitute values into the formula (remember 'c' is the hypotenuse)	A² + B² = C² x² + 24² = 26²
Step 3) Solve for the unknown

Problem 1)

Find the length of X

Step 1

Problem 2)

Use the Pythagorean theorem to calculate the value of X. Round your answer to the nearest tenth.

Step 1

Problem 3)

Use the Pythagorean theorem to calculate the value of X. Round your answer to the nearest hundredth..

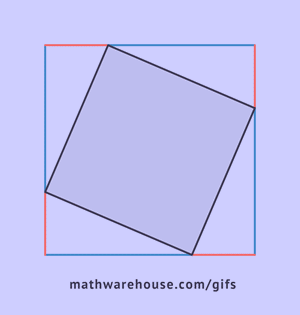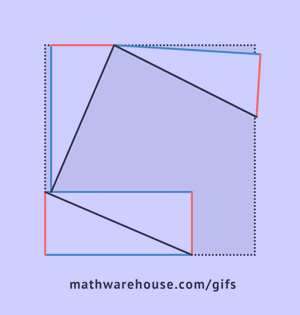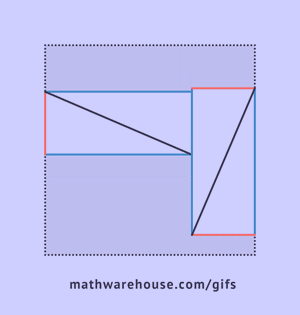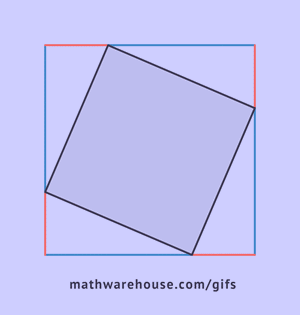
Step 1