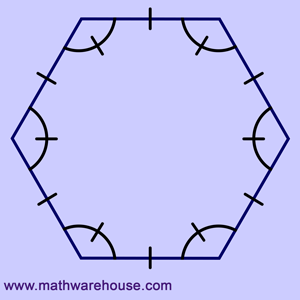
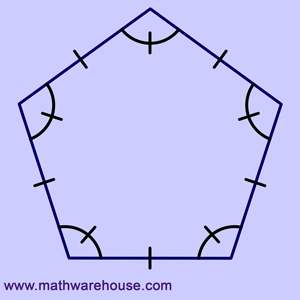
Interior Angle Sum Theorem
What is true about the sum of interior angles of a polygon ?
The sum of the measures of the interior angles of a convex polygon with n sides is $ (n-2)\cdot180^{\circ} $
| Shape | Formula | Sum Interior Angles |
|---|---|---|
|
$$ \red 3 $$ sided polygon
(triangle) |
$$ (\red 3-2) \cdot180 $$ | $$ 180^{\circ} $$ |
|
$$ \red 4 $$ sided polygon
(quadrilateral) |
$$ (\red 4-2) \cdot 180 $$ | $$ 360^{\circ} $$ |
|
$$ \red 6 $$ sided polygon
(hexagon) |
$$ (\red 6-2) \cdot 180 $$ | $$ 720^{\circ} $$ |
Problem 1

180°
You can also use Interior Angle Theorem:$$ (\red 3 -2) \cdot 180^{\circ} = (1) \cdot 180^{\circ}= 180 ^{\circ} $$
Problem 2
360° since this polygon is really just two triangles and each triangle has 180°
You can also use Interior Angle Theorem:$$ (\red 4 -2) \cdot 180^{\circ} = (2) \cdot 180^{\circ}= 360 ^{\circ} $$
Problem 3

Use Interior Angle Theorem:$$ (\red 5 -2) \cdot 180^{\circ} = (3) \cdot 180^{\circ}= 540 ^{\circ} $$
Problem 4
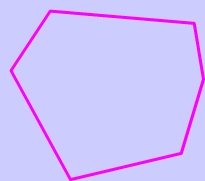
Use Interior Angle Theorem: $$ (\red 6 -2) \cdot 180^{\circ} = (4) \cdot 180^{\circ}= 720 ^{\circ} $$
Video Tutorial
on Interior Angles of a Polygon
Definition of a Regular Polygon:
Measure of a Single Interior Angle
| Shape | Formula | Sum interior Angles |
|---|---|---|
| Regular Pentagon | $$ (\red 3-2) \cdot180 $$ | $$ 180^{\circ} $$ |
|
$$ \red 4 $$ sided polygon
(quadrilateral) |
$$ (\red 4-2) \cdot 180 $$ | $$ 360^{\circ} $$ |
|
$$ \red 6 $$ sided polygon
(hexagon) |
$$ (\red 6-2) \cdot 180 $$ | $$ 720^{\circ} $$ |
What about when you just want 1 interior angle?
In order to find the measure of a single interior angle of a regular polygon (a polygon with sides of equal length and angles of equal measure) with n sides, we calculate the sum interior anglesor $$ (\red n-2) \cdot 180 $$ and then divide that sum by the number of sides or $$ \red n$$.
The Formula$ \text {any angle}^{\circ} = \frac{ (\red n -2) \cdot 180^{\circ} }{\red n} $
Example 1
Let's look at an example you're probably familiar with-- the good old triangle $$\triangle$$ . Now, remember this new rule above only applies to regular polygons. So, the only type of triangle we could be talking about is an equilateral one like the one pictured below.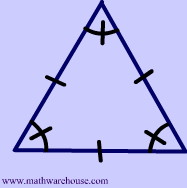
You might already know that the sum of the interior angles of a triangle measures $$ 180^{\circ}$$ and that in the special case of an equilateral triangle, each angle measures exactly $$ 60^{\circ}$$.
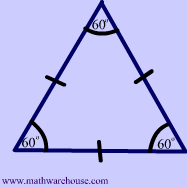 $
\text{Using our new formula}
\\
\text {any angle}^{\circ} = \frac{ (\red n -2) \cdot 180^{\circ} }{\red n}
\\
\text{ For a triangle , (} \red 3 \text{ sides)}
\\ \frac{ (\red 3 -2) \cdot 180^{\circ} }{\red 3}
\\ \frac{ (1) \cdot 180^{\circ} }{\red 3}
\\ \frac{180^{\circ}} {\red 3} = \fbox{60}
$
$
\text{Using our new formula}
\\
\text {any angle}^{\circ} = \frac{ (\red n -2) \cdot 180^{\circ} }{\red n}
\\
\text{ For a triangle , (} \red 3 \text{ sides)}
\\ \frac{ (\red 3 -2) \cdot 180^{\circ} }{\red 3}
\\ \frac{ (1) \cdot 180^{\circ} }{\red 3}
\\ \frac{180^{\circ}} {\red 3} = \fbox{60}
$
So, our new formula for finding the measure of an angle in a regular polygon is consistent with the rules for angles of triangles that we have known from past lessons.
Example 2
To find the measure of an interior angle of a regular octagon, which has 8 sides, apply the formula above as follows: $ \text{Using our new formula} \\ \text {any angle}^{\circ} = \frac{ (\red n -2) \cdot 180^{\circ} }{\red n} \\ \frac{(\red8-2) \cdot 180}{ \red 8} = 135^{\circ} $
Finding 1 interior angle of a regular Polygon
Problem 5
Substitute 8 (an octagon has 8 sides) into the formula to find a single interior angle
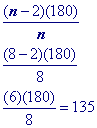
Problem 6
Substitute 12 (a dodecagon has 12 sides) into the formula to find a single interior angle
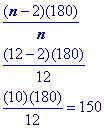
Problem 7
Substitute 16 (a hexadecagon has 16 sides) into the formula to find a single interior angle
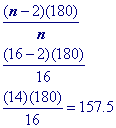
Challenge Problem
This question cannot be answered because the shape is not a regular polygon. You can only use the formula to find a single interior angle if the polygon is regular!
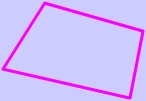
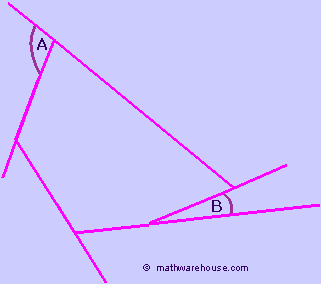
Consider, for instance, the irregular pentagon below.
You can tell, just by looking at the picture, that $$ \angle A and \angle B $$ are not congruent.
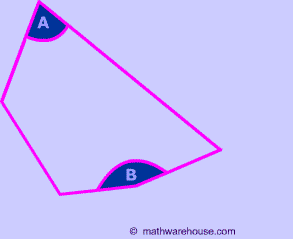
The moral of this story- While you can use our formula to find the sum of the interior angles of any polygon (regular or not), you can not use this page's formula for a single angle measure--except when the polygon is regular.
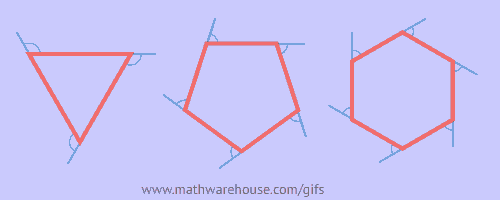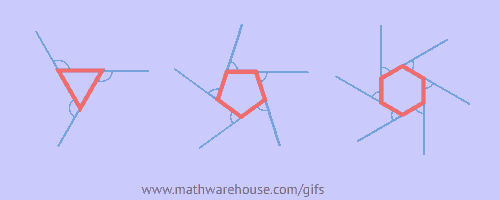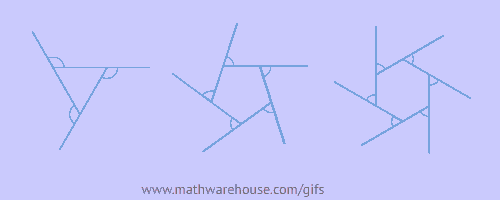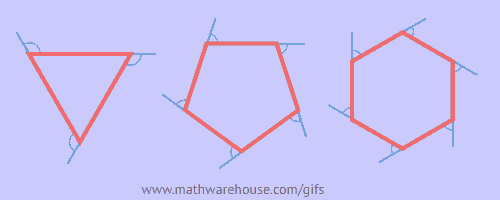
How about the measure of an exterior angle?
Formula for sum of exterior angles:
The sum of the measures of the exterior angles of a polygon, one at each vertex, is 360°.
Measure of a Single Exterior Angle
Formula to find 1 angle of a regular convex polygon of n sides = ![]()
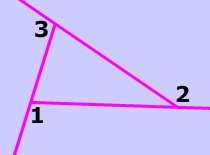
$$ \angle1 + \angle2 + \angle3 = 360° $$
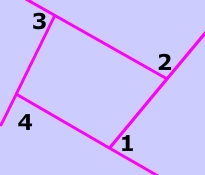
$$ \angle1 + \angle2 + \angle3 + \angle4 = 360° $$
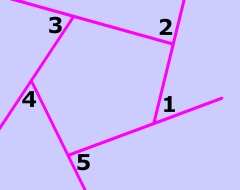
$$ \angle1 + \angle2 + \angle3 + \angle4 + \angle5 = 360° $$
Practice Problems
Problem 8
Substitute 5 (a pentagon has 5sides) into the formula to find a single exterior angle
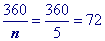
Problem 9
Substitute 10 (a decagon has 10 sides) into the formula to find a single exterior angle
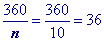
Problem 10
Substitute 12 (a dodecagon has 12 sides) into the formula to find a single exterior angle
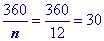
Challenge Problem
This question cannot be answered because the shape is not a regular polygon. Although you know that sum of the exterior angles is 360, you can only use formula to find a single exterior angle if the polygon is regular!
Consider, for instance, the pentagon pictured below. Even though we know that all the exterior angles add up to 360 °, we can see, by just looking, that each $$ \angle A \text{ and } and \angle B $$ are not congruent..
Determine Number of Sides from Angles
It's possible to figure out how many sides a polygon has based on how many degrees are in its exterior or interior angles.
Problem 11
Use formula to find a single exterior angle in reverse and solve for 'n'.
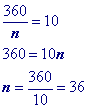
Problem 12
Use formula to find a single exterior angle in reverse and solve for 'n'.
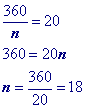
Problem 13
Use formula to find a single exterior angle in reverse and solve for 'n'.
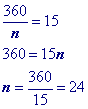
Challenge Problem
When you use formula to find a single exterior angle to solve for the number of sides , you get a decimal (4.5), which is impossible. Think about it: How could a polygon have 4.5 sides? A quadrilateral has 4 sides. A pentagon has 5 sides.