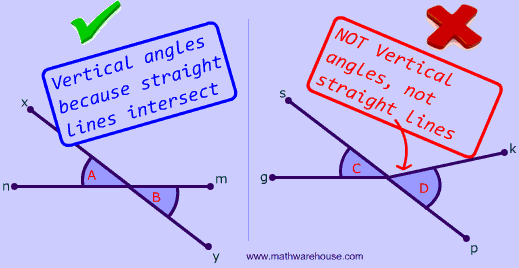
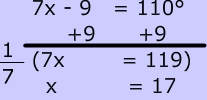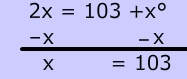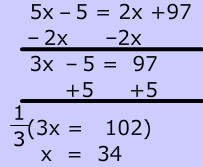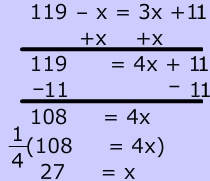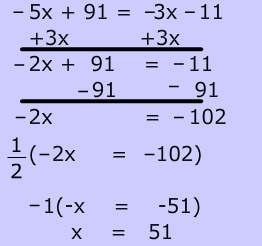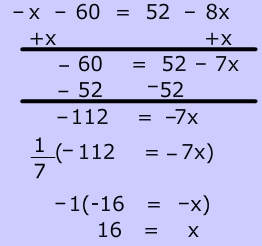Click and the points below to see the rule for vertical angles in action.
| ∠ A | 90 |
|---|---|
| ∠ B | 90 |
Drag Points Of The Lines To Start Demonstration
Related:
What are Vetical Angles?
Vertical angles are the angles that are opposite each other when two straight lines intersect. (Technically, these two lines need to be on the same plane)
Vertical angles are congruent(in other words they have the same angle measuremnt or size as the diagram below shows.)
Diagram 1
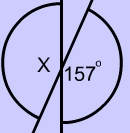
m$$ \angle x $$ in digram 1 is $$ 157^{\circ}$$ since its vertical angle is $$ 157^{\circ}$$.
Picture 1
Picture 2
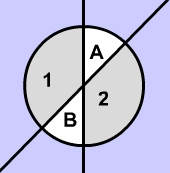
In Picture 2, $$ \angle $$ 1 and $$ \angle $$2 are vertical angles. Likewise, $$ \angle $$A and $$ \angle $$ B are vertical. Vertical angles are always congruent (have the same measure).
Picture 3
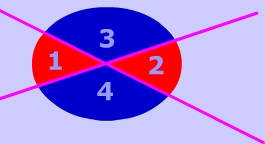
Picture 3 is another picture of vertical angles. The blue pair and red pair of angles are congruent pairs of vertical angles.
Interactive Vertical Angles
Practice Problems
Use the theorem that vertical angles are congruent to find the value of x in the problems below.
Problem 1
What is the m $$ \angle $$ B ?
Angle B is $$ 130° $$
Example 2
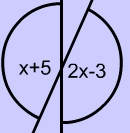
Vertical Angle problems can also involve algebraic expressions. To find the value of x, set the measure of the 2 vertical angles equal, then solve the equation: $ x + 4 = 2x-3 \\ x= 8 $
Problem 2
What is the value of x?
$ x -2 = 133 \\ x = 133 + 2 \\ x = \boxed{ 135} $
Problem 3
What is the value of x?
$ 2x + 5 = 105 \\ 2x = 100 \\ \frac 1 2 (2x) = \frac 1 2 (100) \\ x = \boxed{ 50} $
Problem 4
Use the vertical angles theorem to solve for x
$ 4x + 7 = 131 \\ 4x = 124 \\ \frac 1 4 (4x) = \frac 1 4 (124) \\ x = \boxed{ 31} $
Problem 5
Find the value of x?
Problem 6
Use your knowledge of vertical angles to solve for x
Problem 7
Solve for x
Problem 8
Use vertical angles to find the value of x
Problem 9
Use vertical angles to find the value of x
Problem 10
Use vertical angles to solve for x
Related:
