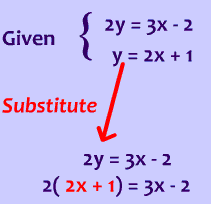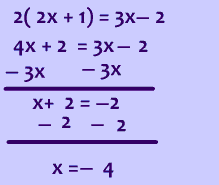How to solve systems of linear equations by substitution, examples, pictures, practice. Step is to ..

The Substitution Method

First, let's review how the substitution property works in general.

Review Example 1

Review Example 2

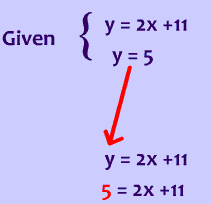
Substitution Example 1

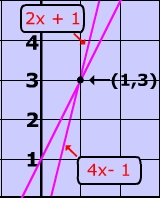
Let's re-examine system pictured up above.

$ \red{y} = 2x + 1 \text{ and } \red{y} = 4x -1 $

Step 1

We are going to use substitution like we did in review example 2 above.

Now we have 1 equation and 1 unknown, we can solve this problem as the work below shows.

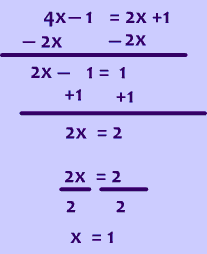
The last step is to again use substitution, in this case we know that x = 1, but in order to find the y value of the solution, we just substitute x = 1 into either equation.

$$ y = 2x + 1 \\ y = 2\cdot \red{1} + 1 = 2 + 1 =3 \\ \\ \boxed{ \text{ or you use the other equation}} \\ y = 4x -1 \\ y = 4\cdot \red{1}- 1 \\ y = 4 - 1 = 3 \\ \boxed { ( 1,3) } $$

Substitution Example 2

What is the solution of the system of equations below:

$ y = 2x + 1 \\ 2y = 3x - 2 $

Step 1

Identify the best equation for substitution and then substitute into other equation.

Step 2

Solve for x

Step 3

Substitute the value of x (-4 in this case) into either equation.

$$ y = 2x + 1 \\ y = 2\cdot \red{-4} + 1 = -8 + 1 = -7 \\ 2y = 3x - 2\\ 2y = 3\cdot-4 -2 \\ \boxed{ \text{ or you use the other equation}} \\ 2y = 3x -2 \\ 2y = 3 ( \red{-4}) -2 \\ 2y = -12 -2 \\ 2y = -14 \frac{1}{2}\cdot2y =\frac{1}{2}\cdot-14 \\ y = -7 $$

$$ \boxed { ( -4, -7 ) } $$

You can also solve the system by graphing and see a picture of the solution below:

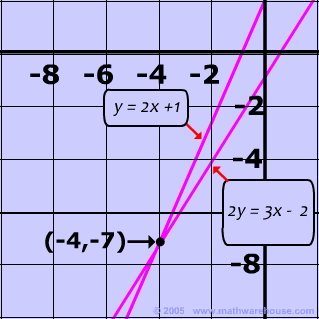
Substitution Practice Problems

Problem 1

Solve the system below using substitution

$$ y = x+1 \\ y = 2x +2 $$

The solution of this system is the point of intersection: (-1, 0).

$$ y = x + 1 \quad y = 2x + 2 \\ \hspace{1.2cm} \downarrow \hspace{1.4cm} \downarrow \\ \hspace{6mm} x + 1 = 2x + 2 \\ \hspace{7mm} \text{-}x \hspace{1.4cm} \text{-}x \\ \hspace{7mm} \rule{3.2cm}{0.25mm} \\ \hspace{1.7cm} 1 = x + 2 \\ \hspace{1.6cm} \text{-}2 \hspace{1.4cm} \text{-}2 \\ \hspace{7mm} \rule{3.2cm}{0.25mm} \\ \hspace{1.2cm} -1 = x \\ \hspace{1.6cm} \downarrow \\ \hspace{5mm} y = 2x + 2 \\ \hspace{7mm} y = 2 * (-1) + 2 = 0 \\[5mm] \text{Solution:} \hspace{3mm} (-1, 0) $$

Problem 2

Use substitution to solve the following system of linear equations:

Line 1: y = 3x – 1
Line 2: y = x – 5

Step 1

Set the Two Equations equal to each other then solve for x

Step 2

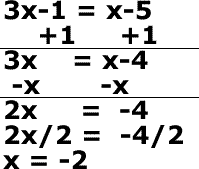
Substitute the x value, -2, into the value for 'x' for either equation to determine y coordinate of solution

$$ y = \red{x} -5 \\ y = \red{-2} -5 = -7 $$

The solution is the point (-2, -7)

Problem 3

Use the substitution method to solve the system:

Line 1: y = 5x – 1
Line 2: 2y= 3x + 12

Solution of system of equations by substitution method

This system of lines has a solution at the point (2, 9).

Problem 4

Use substitution to solve the system:

Line 1: y = 3x + 1
Line 2: 4y = 12x + 4

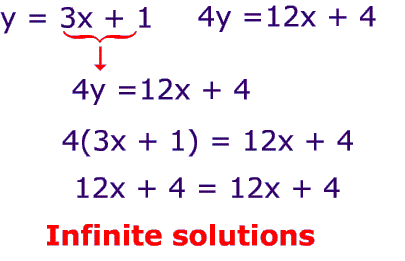
Infinite Solutions of system of equations by substitution method

This system has an infinite number of solutions. Because 12x + 4 = 12x is always true for all values of x.

Problem 5

Solve the system of linear equations by substitution

Line 1: y= x + 2
Line 2: y= x + 8

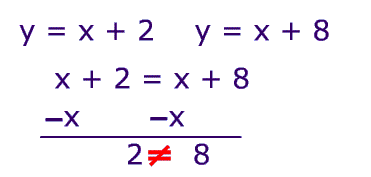
Practice Problem Nine solution of system of equations

This system of linear equation has no solution.

These lines have the same slope (slope = 1) so they never intersect.

Problem 6

Use the substitution method to solve the system:

Line 1: y = x + 1
Line 2: 2y = 3x

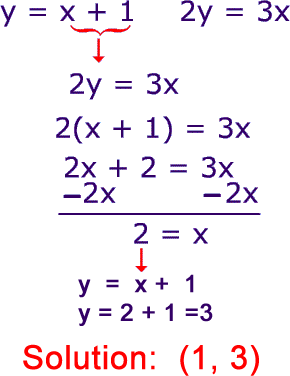
The solution of this system is (1, 3).

Problem 7

Use substitution to solve the system:

Line 1: y = 3x + 1
Line 2: 4y = 12x + 3

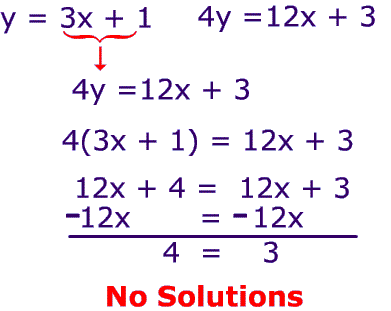
No Solutions of system of equations by substitution method

Whenever you arrive at a contradiction such as 3 = 4, your system of linear equations has no solutions.
When you use these methods (substitution, graphing, or elimination) to find the solution what you're really asking is at what

This system has no solutions.