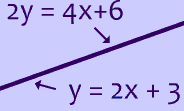What is a system of equations?
AnswerA system of equation just means 'more than 1 equation.'. A system of linear equations is just more than 1 line, see the picture:
Ok, so what is the solution of a system of equations?
AnswerThe solution is where the equations 'meet' or intersect. The red point is the solution of the system.
How many solutions can systems of linear equations have?
AnswerThere can be zero solutions, 1 solution or infinite solutions--each case is explained in detail below. Note: Although systems of linear equations can have 3 or more equations,we are going to refer to the most common case--a stem with exactly 2 lines.
Case I: 1 Solution
This is the most common situation and it involves lines that intersect at exactly one point.
Case 2: No Solutions
This only happens when the lines are parallel. As you can see, parallel lines are not going to ever meet.
Example of a stem that has no solution:
- Line 1: $$ y = 5x + 13 $$
- Line 2: $$ y = 5x + 12 $$
Case III: Infinite Solutions
This is the rarest case and only occurs when you have the same line
Consider, for instance, the two lines below (y = 2x + 1 and 2y = 4x + 2). These two equations are really the same line.
Example of a system that has infinite solutions:
- Line 1: y = 2x + 1
- Line 2: 2y = 4x + 2
How can we find solutions to systems of equations?
To find the solution to systems of linear equations, you can any of the methods below:
