Parallel Lines in Greater Depth
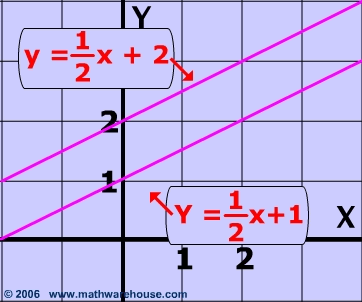
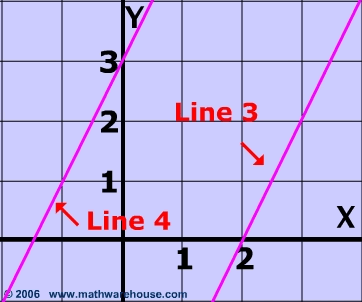
Both of the lines below have the same slope : $$ \frac{1}{2} $$
Therefore these lines are parallel and will never meet.
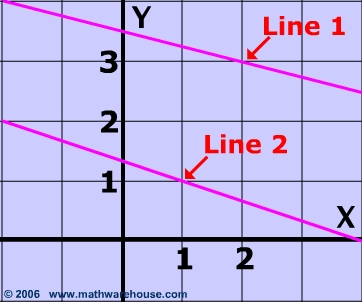
Problem 1
Are the two lines pictured below parallel?
Show Answer
No.
While these lines may look parallel at first glance, if you look closely and calculate each line's slope , you will find that:
line 1 has a slope of $$ -\frac{1}{4} $$
line 2 's slope is $$ - \frac{1}{3} $$
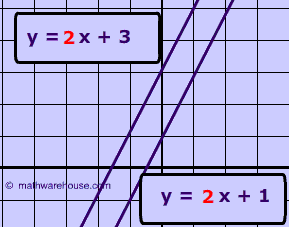
Problem 2
Are the two lines below parallel?
Show Answer
slope , 2, and clearly are never going to intersect.
Perpendicular Lines in Greater Depth
Perpendicular lines:
intersect at $$ 90^{\circ} $$
have slopes that are negative reciprocals
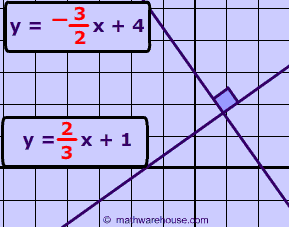
Problem 3
Are the two lines in the picture below perpendicular?
Show Answer
Yes
The slope of line 1 is -2 and that of line 2 is $$ \frac{1}{2}$$ .
-2 and $$ \frac{1}{2}$$ are negative reciprocals so the lines are perpendicular.
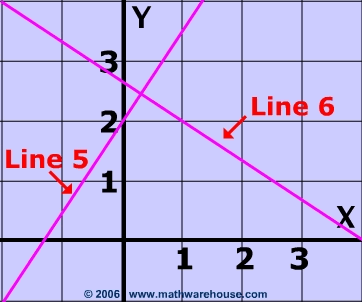
Problem 4
Determine whether or not lines 6 and 5 perpendicular?
Show Answer
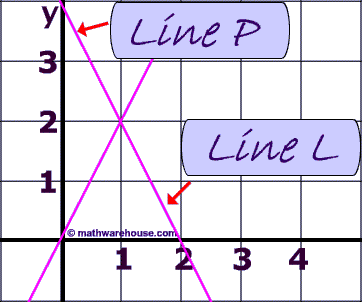
Problem 5
Are line P and line L perpendicular?
Show Answer