|
|
|
|
|
|
 
|
Absolute Value of a Complex NumberHow to calculate a complex number's absolute value The absolute value of a real number is its distance from 0 on the number line. A complex number's absolute value is also a measure of its distance from zero. However, instead of measuring this distance on the number line, a complex number's absolute value is measured from zero on the complex number plane.
In general
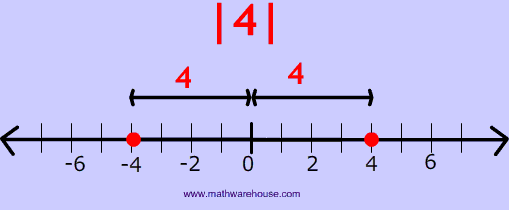
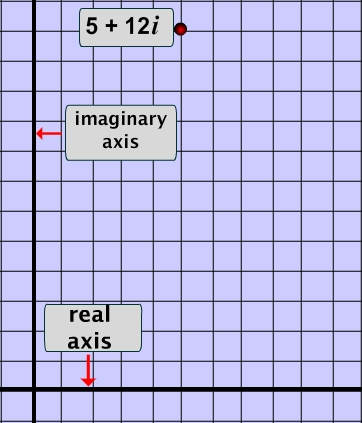
Illustrated Example
Practice Problems
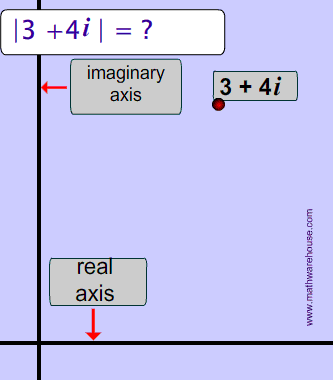
To find the absolute value of the complex number, 3 + 4i, we find the distance from zero to that number on the plane.
Calculate |5+ 12i|
answer
Answer3 
What is | 6 + 8i| ?
Related Page:how to simplify imaginary number |complex number introduction| solving equations with complex numbers Top |
